Similar Questions
Explore conceptually related problems
Recommended Questions
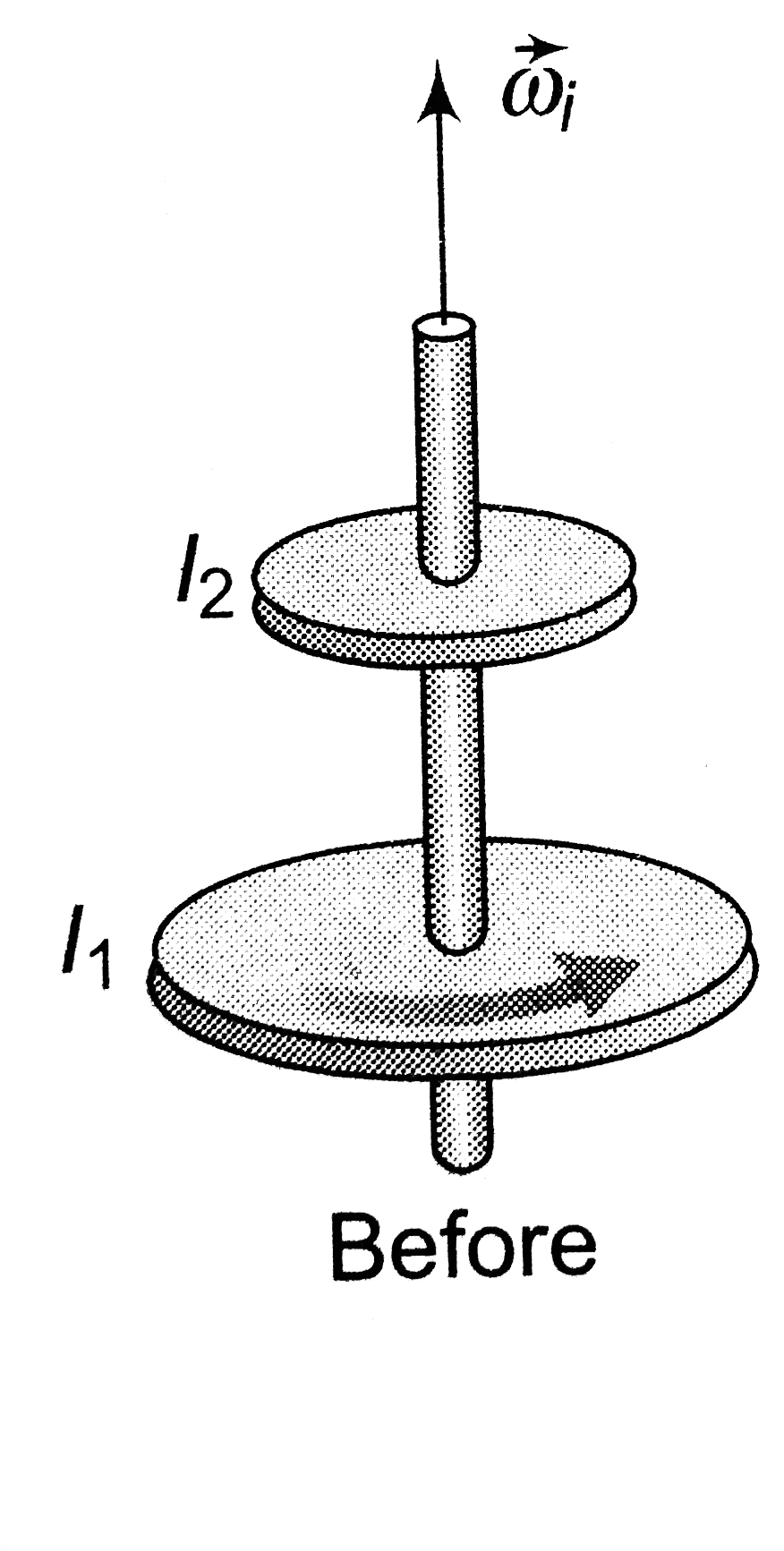
- A disk with moment of inertia I1 rotates about frictionless, vertical ...
Text Solution
|
- A disk with moment of inertia I1 rotates about frictionless, vertical ...
Text Solution
|
- Two bodies with moment of inertia I1 and I2 (I1 gt I2) have equal angu...
Text Solution
|
- A circular disc of moment of inertia I(t) is rotating in a horizontal...
Text Solution
|
- Two bodies with moment of inertia I1 and I2 (I2 gt I1) are rotating wi...
Text Solution
|
- A thin circular disk of radius R is uniformly charged with density sig...
Text Solution
|
- एक ही अक्ष के परितः घूर्णन कर रही दो वस्तुआ A तथा B के जड़त्व आघूर्...
Text Solution
|
- एक ही अक्ष के परितः घूर्णन कर रही दो वस्तुआ A तथा B के जड़त्व आघूर्...
Text Solution
|
- I(a) நிலைமத் திருப்புத் திறன் கொண்ட வட்டத்தட்டு மாறாத கோண திசைவேகம் om...
Text Solution
|
 .
.