Similar Questions
Explore conceptually related problems
Recommended Questions
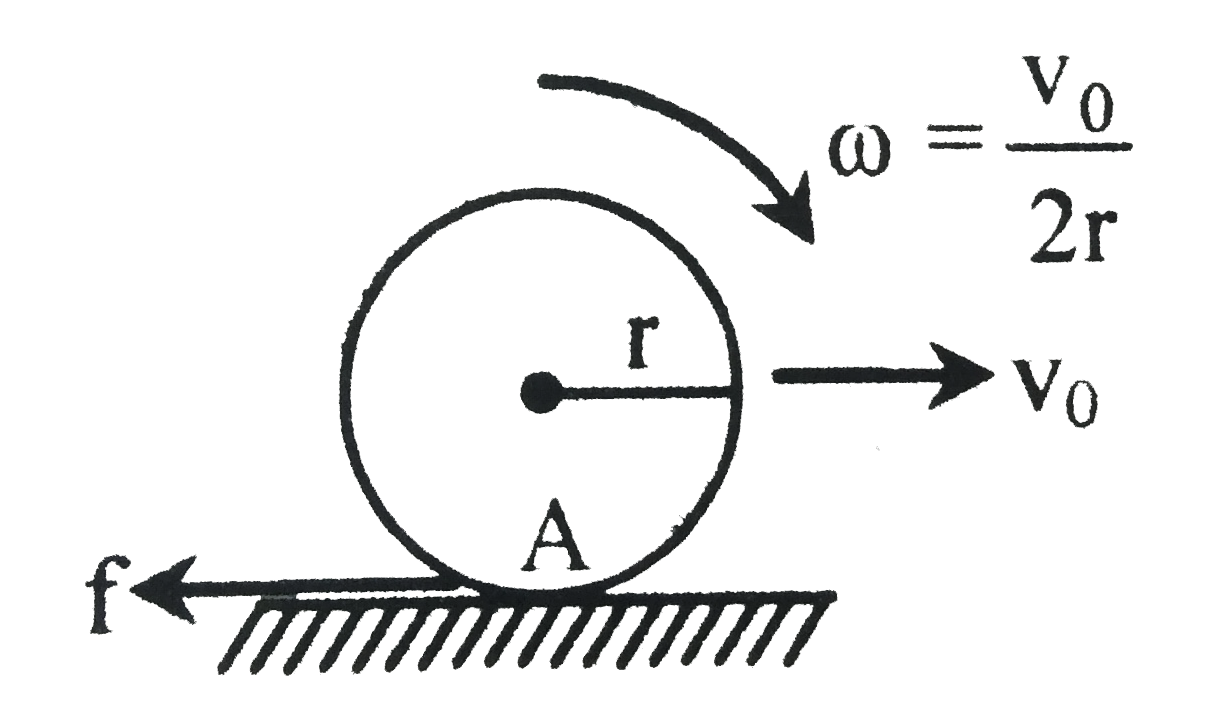
- A sphere of mass M and radius r shown in figure slips on a rough horiz...
Text Solution
|
- A sphere of mass M and radius r shown in figure slips on a rough horiz...
Text Solution
|
- A uniform ring of radius R is given a back spin of angular velocity V(...
Text Solution
|
- A solid sphere and a hollow sphere of equal mass and radius are placed...
Text Solution
|
- A sphere of mass M and radius r shown in the figure on a rough horizon...
Text Solution
|
- A sphere of mass M and radius r shown in figure slips on a rough horiz...
Text Solution
|
- Consider a hollow sphere rolling with slipping with velocities as show...
Text Solution
|
- A sphere of mass M and radius r slips on a rough horizontal plane. At ...
Text Solution
|
- A sphere of mass m and radius R is kept on a rough floor. A sharp impu...
Text Solution
|
 .
.