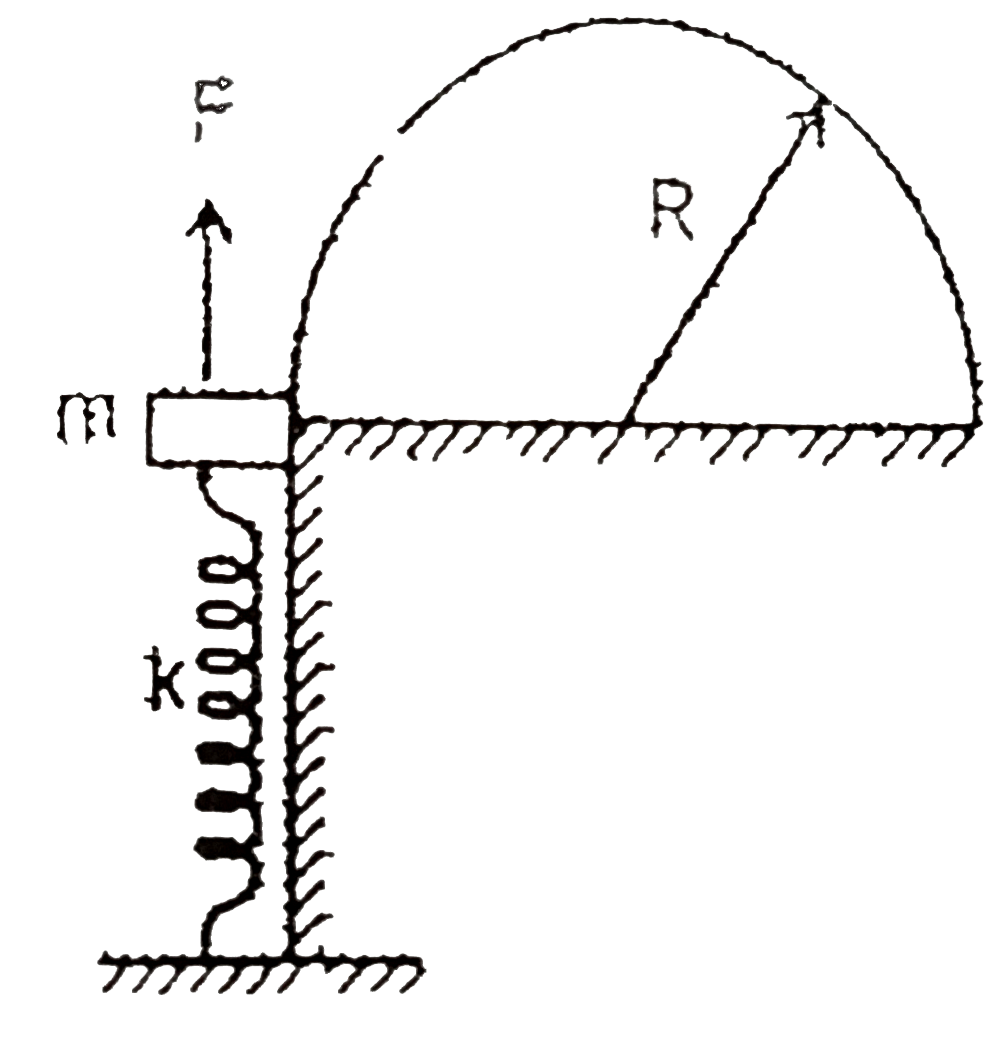Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
FIITJEE-WORK, ENERGY & POWER-Example
- In the figure shown a semi-cylinder of radius, R is rigidly fixed on a...
Text Solution
|
- A spring mass system is held at rest with the spring relaxed at a heig...
Text Solution
|
- The arrangement shown in the diagram is moving in space with an accele...
Text Solution
|
- The system of mass A and B shown in the figure is released from rest w...
Text Solution
|
- A wedge with a rough circular track AB, is fixed on the plane x x'. Th...
Text Solution
|
- Two bodies A and B of each of mass 100 gm are allowed to move along a ...
Text Solution
|
- A particle is moving on a circle of radius R such that at every instan...
Text Solution
|
- A force given by the relation F=8t, acts on a body of mass 2 kg, initi...
Text Solution
|
- A particle of mass m is moving horizontally with a constant velocity v...
Text Solution
|
- A body is acted upon by a force which is inversely proportional to the...
Text Solution
|
- A machine delivers power to a body which is proportional to velocity o...
Text Solution
|
- The kinetic energy acquired by a mass m travelling a certain distance ...
Text Solution
|
- A particle of mass m slides on a frictionaless surface ABCD, starting ...
Text Solution
|
- A projectile is fired with some velocity making certain angle with the...
Text Solution
|
- A force shown in the F-x graph is applied to a 2kg block horizontal as...
Text Solution
|
- The potential energy function for the force between two in a diatomic ...
Text Solution
|
- The potential energy function for the force between two in a diatomic ...
Text Solution
|
- The potential energy function for the force between two in a diatomic ...
Text Solution
|