Home
Class 11
PHYSICS
A spaceship is sent to investigate a pla...

A spaceship is sent to investigate a planet of mass `M` and radius `R`. While hanging motionless in space at a distance `5R` from the centre of the planet, the spaceship fires an instrument package of mass `m`, which is much smaller than the mass of the spaceship. For what angle `theta` will the package just graze the surface of the planet?

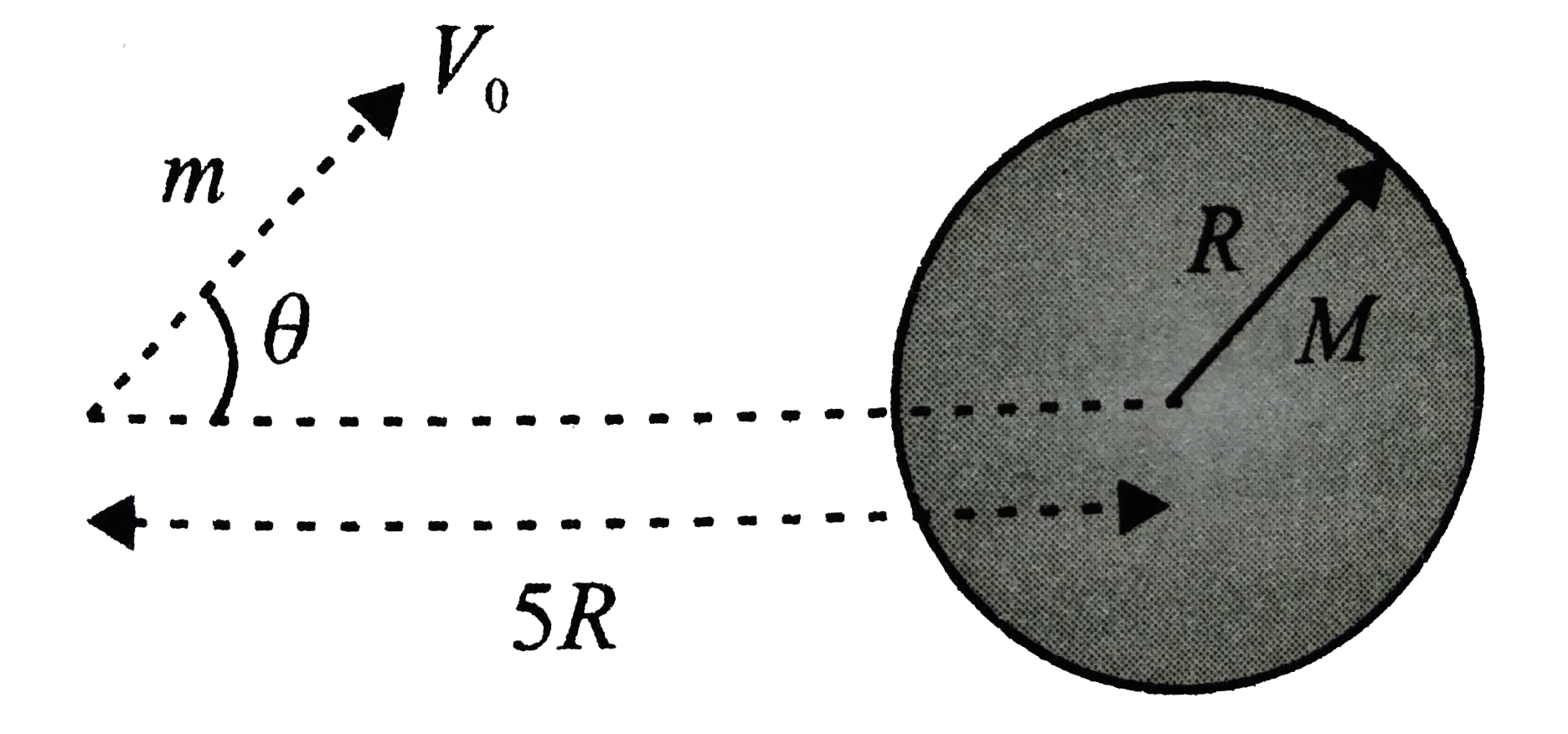
Text Solution

Verified by Experts

Let the speed of the instruement package is `v` when it grazes the surface of the planet.
Conserving angular momentum of the package about the centre of the planet
`mv_(0)xx5Rsin(pi-theta)=mvRsin90^(@)`
Conserving mechanical energy,
`-(GMm)/(5R)+(1)/(2)mv_(0)^(2)=-(GMm)/(R )+(1)/(2)mv^(2)`
`rArr (1)/(2)m(v^(2)-v_(0)^(2))=(4GMm)/(5R)`
`v^(2)-v_(0)^(2)=(8GM)/(5R)`
Subsituting the value of `v` from Eq. `(1)` in Eq. `(2)`
`25v_(0)^(2)sin^(2)theta-v_(0)^(2)=(8GM)/(5R)`
`rArr sintheta=(1)/(5)sqrt(1+(8GM)/(5v_(0)^(2)R))`
or `theta=sin^(-1)[(1)/(5)sqrt((1+(8GM)/(5v_(0)^(2)R)))]`
Promotional Banner

Topper's Solved these Questions

  • FLUID MECHANICS

    FIITJEE|Exercise Example|14 Videos

  • HEAT & THERMODYNAMICS

    FIITJEE|Exercise Example|14 Videos

Similar Questions

Explore conceptually related problems

A particle at a distance r from the centre of a uniform spherical planet of mass M radius R (ltr) has a velocity of magnitude v.

The angular velocity of rotation of a planet of mass M and radius R, at which the matter start to escape from its equator is

A space vehicle approaching a planet has a speed v when it is very far from the planet At that moment tangent of its trajectory would miss the centre of the planet by distance R if the planet has mass M and radius r what is the smallest value of R in order that the resulting orbit of the space vehicle will just miss the surface of the planet?

If v_(e) is the escape velocity of a body from a planet of mass 'M' and radius 'R . Then the velocity of the satellite revolving at height 'h' from the surface of the planet will be

A body of mass m at inifnity is approaching the centre of a hypothetical hollow planet of mass M and radius R . The speed of the body when it passes the centre of the planet through a diametrical tunnel is

A small asteroid is approaching a planet of mass M and radius R from a large distance. Initially its velocity (u) is along a tangent to the surface of the planet. It fall on the surface making an angle of 30^(2) with the vertical. Calculate u.

A planet has a mass M_(1) and radius R_(1). The value of acceleration- due to gravity on its surface is g_(1). There is another planet 2, whose mass and radius both are two times that of the first planet. Which one of the following is the acceleration due to gravity on the surface of planet 2?

At satellite of mass m is launched from the surface of a planet of mass M and radius R in a circular orbit at an altitude of 3R. K.E. of satellite at the time of launching is

The earth is a homogeneous sphere of mass M and radius R. There is another spherical planet of mass M and radius R whose density changes with distance r from the centre as p=p_(0)r. (a) Find the ratio of acceleration due to gravity on the surface of the earth and that on the surface of the planet. (b) Find p_(0).