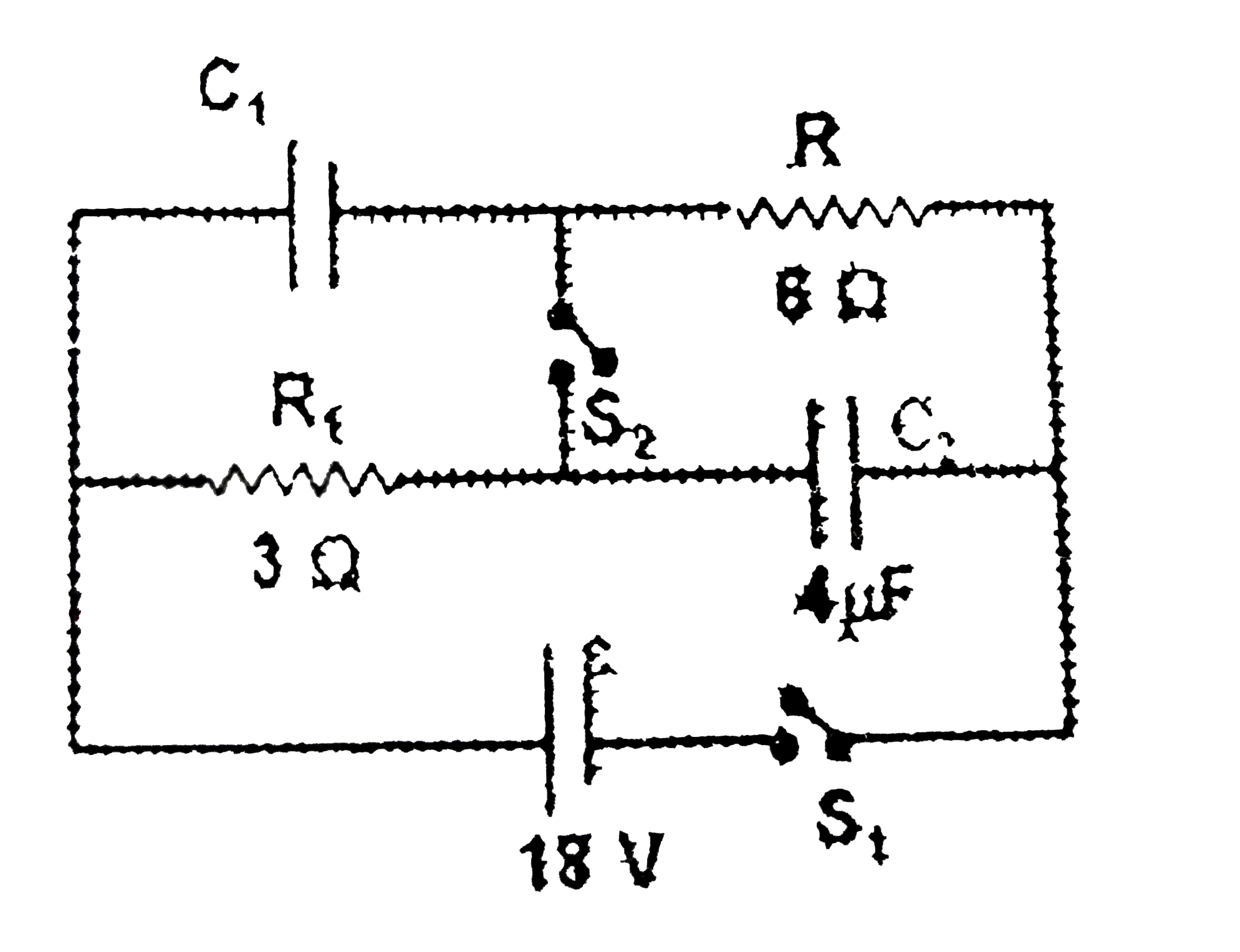
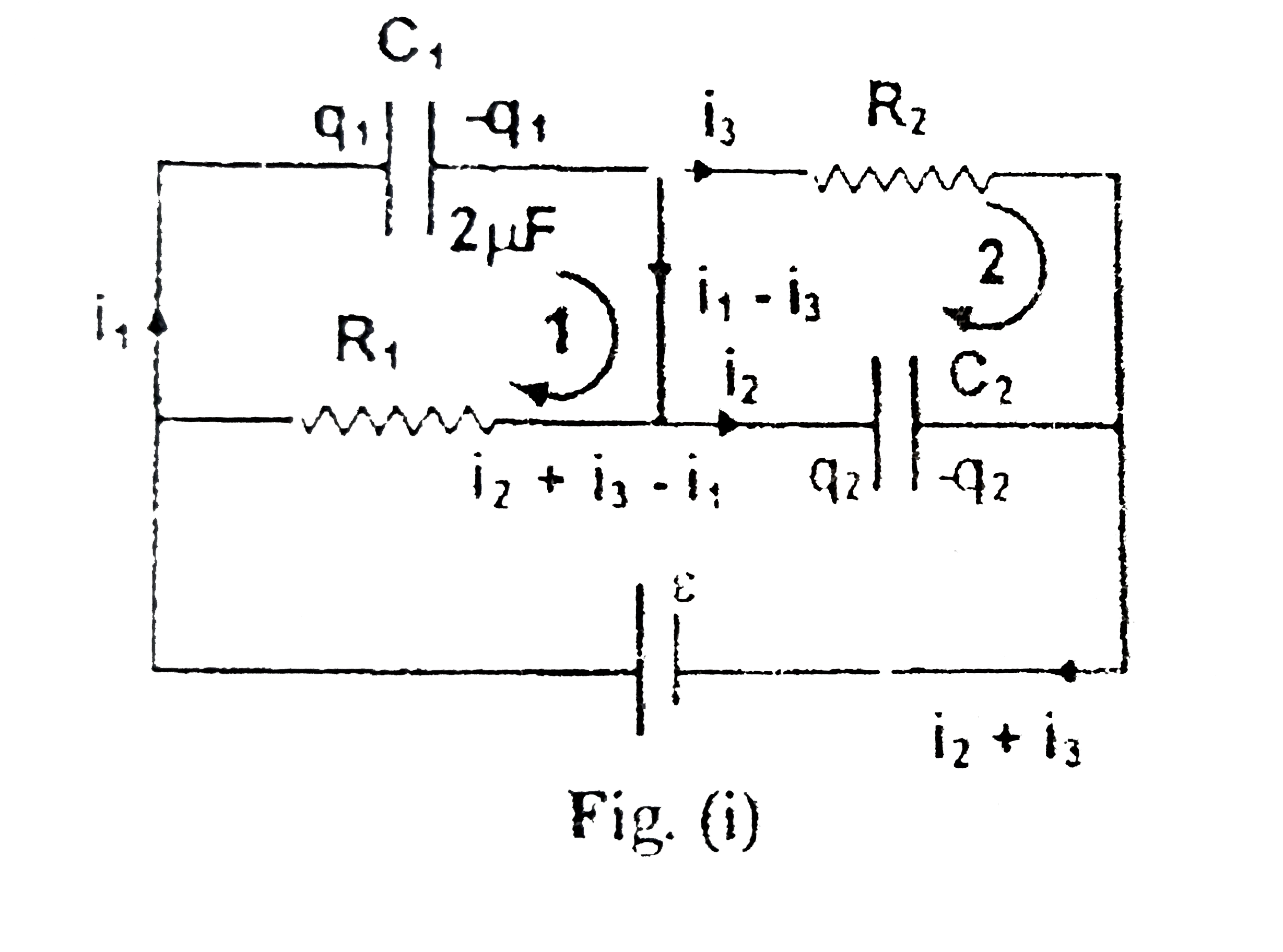Consider the charges on capacitors and currents through various branches, as shown in the figure
For loop `1`, we have
`R_(1)(I_(2)+I_(3)-I_(1))=(q_(1))/(C_(1))` `(1)`
For loop`2`, `R_(2)i_(3)=(q_(2))/(C_(1))` `(2)`
For the outer loop, `i_(3)R_(2)+(q_(1))/(C_(1))=epsilon` `(3)`
Also, `i_(1)=(dq_(1))/(dt)` and `i_(2)=(dq_(2))/(dt)` `(4)`
Putting the values of `i_(1)` and `i_(2)` from Eq. `(4)` and of `i_(3)` from Eq. `(2)` in `(1)`, we get
`(d)/(dt)(q_(2)-q_(1))=(q_(1))/(R_(1)C_(1))-(q_(2))/(R_(2)-C_(2))` `(5)`
From Eqs. `(2)` and `(3)`, we get
`(q_(2))/(C_(2))+(q_(1))/(C_(1))=epsilon` `(6)`
From Eqs. `(5)` and `(6)`, we get
`int_(0)^(q_(2))(dq_(2))/(((epsilonC_(2)R_(2))/(R_(1)+R_(2)))-q_(2))=int_(0)^(t)(dt)/(R_(eq)(C_(1)+C_(2)))`, where `R_(eq)=(R_(1)R_(2))/(R_(1)+R_(2))`
`rArrq_(2)=(epsilonR_(2)C_(2))/((R_(1)+R_(2)))[1-e^((1)/(R_(eq)(C_(1)+C_(2))))]`
Similarly, `q_(1)=(epsilonR_(1)C_(1))/((R_(1)+R_(2)))[1-e^((1)/(R_(eq)(C_(1)+C_(2))))]`
`rArr i_(1)=(dq_(1))/(dt)=(epsilonC_(1))/(R_(2)(C_(1)+C_(2)))e^((1)/(R_(eq)(C_(1)+C_(2))))`
Similarly, `i_(2)=(epsilonC_(2))/(R_(1)(C_(1)+C_(2)))e^((-1)/(R_(eq)(C_(1)+C_(2))))`
From equation `(1)`
Current through `S_(2)=(i_(1)-i_(3))=i_(2)-(q_(1))/(R_(1)C_(1))`
Putting the values, we get
`q_(1)=(12muC)(1-e^((1)/(12mu)))`, `q_(2)=(48muC)(1-e^((1)/(12mu)))`
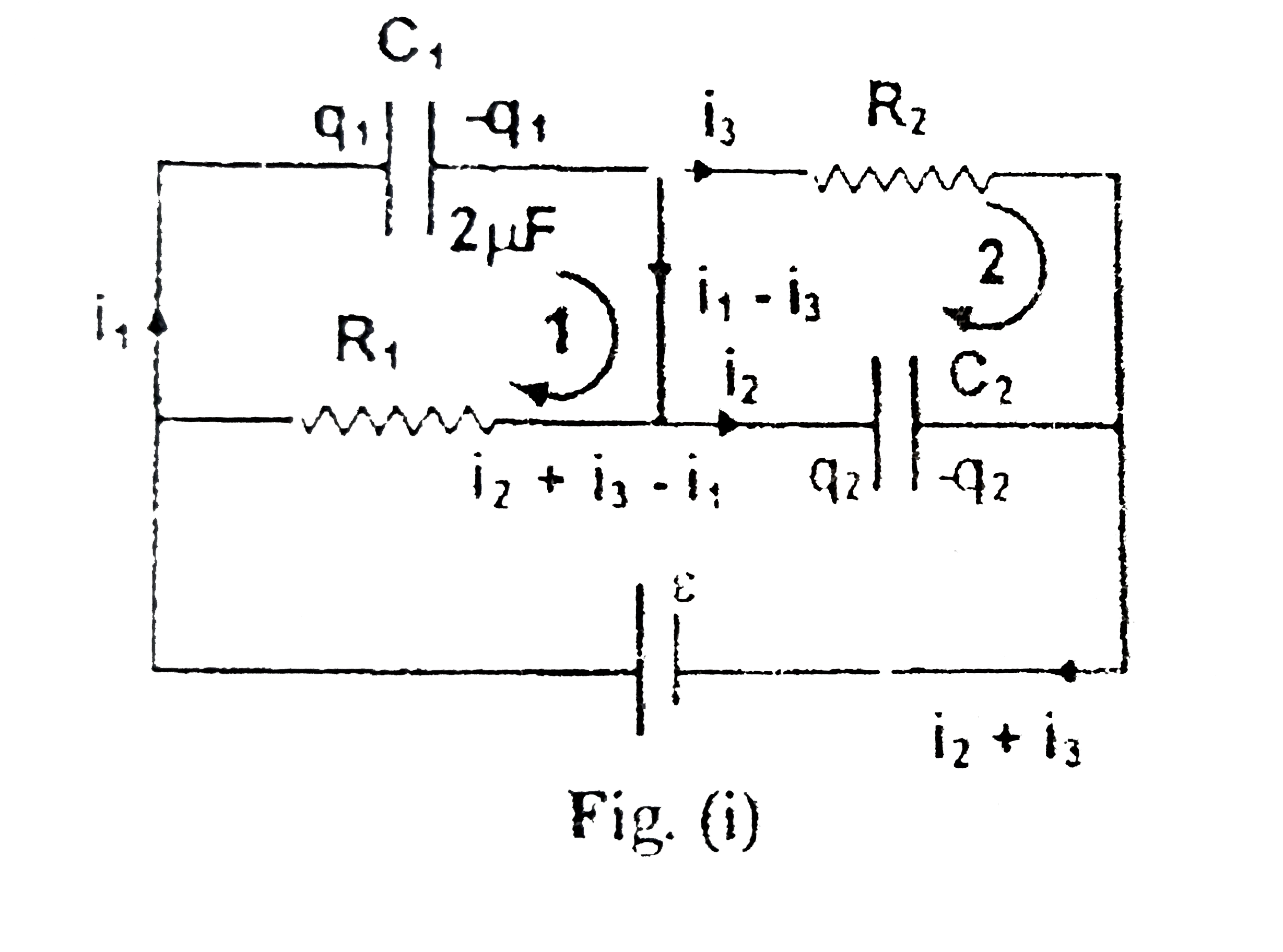
`i_(1)=(1A)e^((1)/(12mu))`, `i_(2)=(4A)e^((1)/(12mu))`
Current through switch `s_(2)=-[2-e^((1)/(12mu))]A` along the indicated direction as shown in fig `(i)`,
With both the switches closed the steady state charges and currents are as shown in Fig `(ii)`.
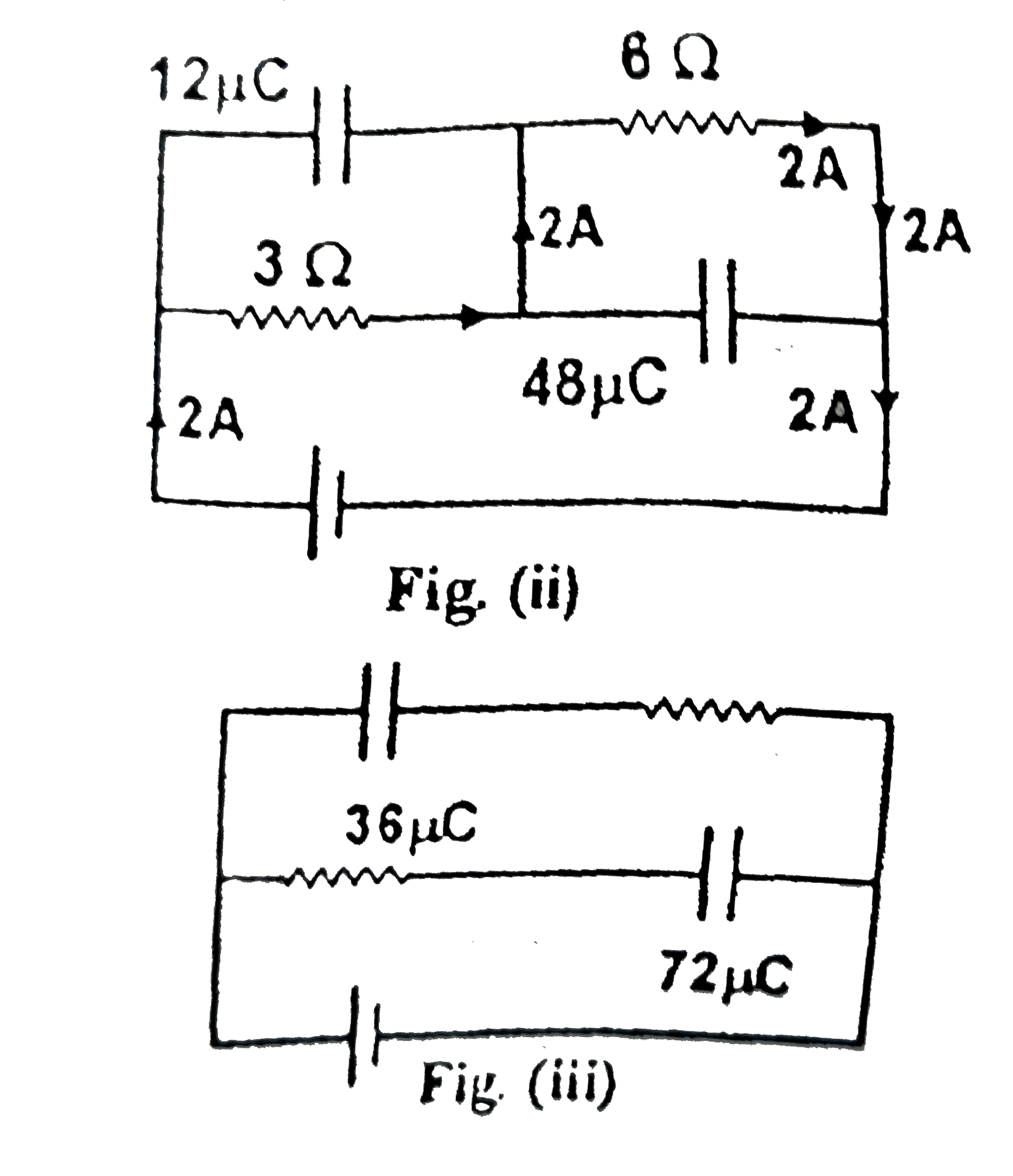
With switch `S_(2)` open and `s_(1)` closed, the steady state charges are as shown in Fig.`(iii)`.
Hence, the charge flown through switch `S_(1)=[(36+72)-(12+48)]muC=48muC`.
Total heat dissipated in the resistors `=` [Initial energy `+` work done by battery when `48muC` flows through it after switch `S_(2)` is opened ] `-` [final energy]
`={(1)/(2)C_(1)V_(1)^(2)+(1)/(2)C_(2)V_(2)^(2)}+epsilon(DeltaQ)-{(1)/(2)C_(1)V'_(1)^(2)+(1)/(2)C_(2)V'_(2)^(2)}=136muJ`.