Home
Class 12
PHYSICS
Light of wavelengthlambda = 500 nm falls...

Light of wavelength`lambda = 500 nm` falls on two narrow slits placed a distance d = ` 50 xx 10^-4` cm
apart, at an angle `phi= 30^@` relative to the slits as shown in figure. On the lower slit a transparent slab of thickness 0.1 mm and refractive index `3/2` is placed. The interference pattern is observed at a distance D=2m from the slits. Then, calculate

(a) position of the central maxima.
(b) the order of maxima at point C of screen .
(c)how many fringes will pass C, if we remove the transparent slab from the lower slit?

Text Solution

Verified by Experts

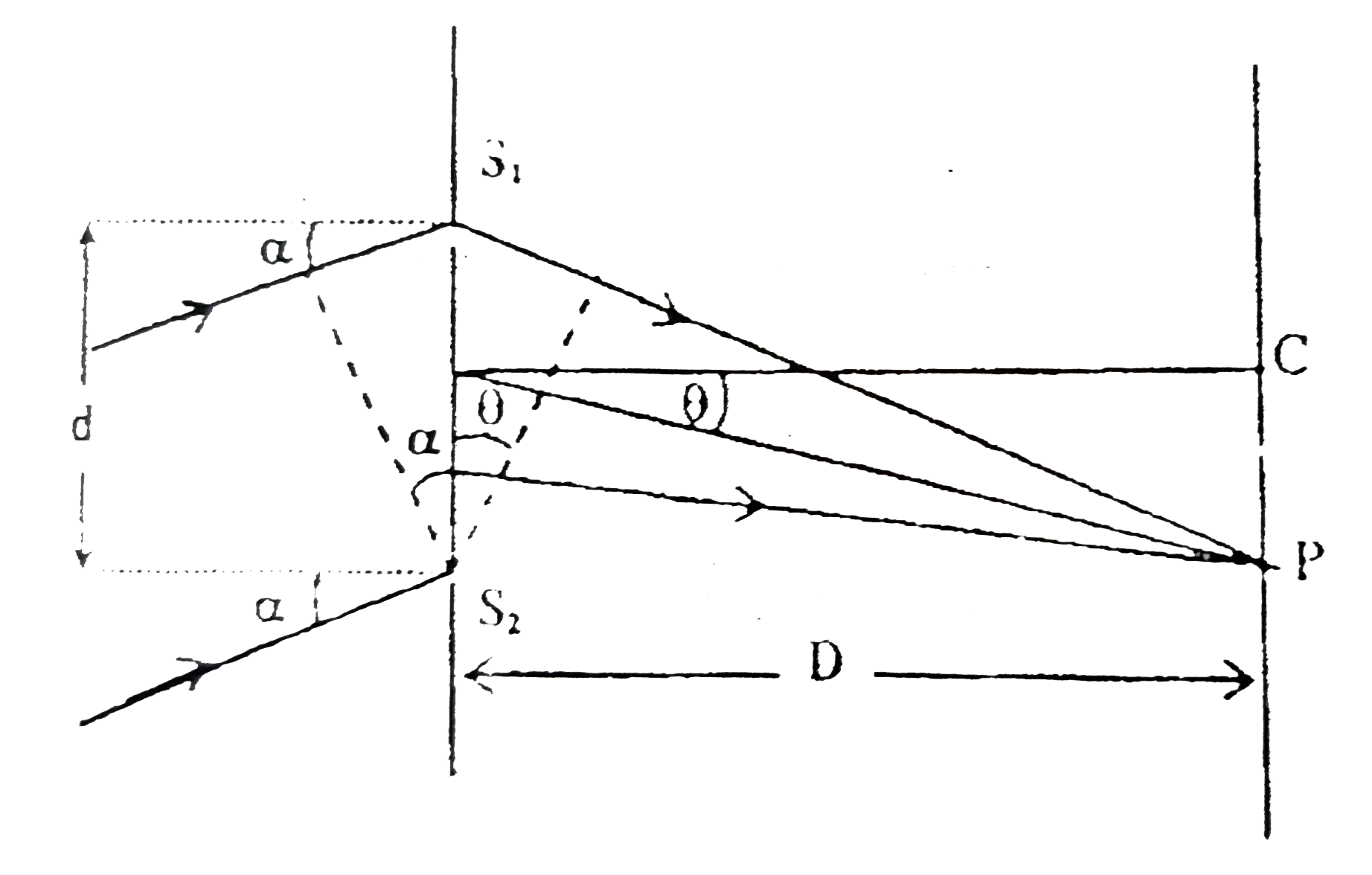
Phase difference `Deltaphi=kd sinphi+kd sinphi+kb(1-n)`, where `k=(2pi)/(lambda)`
Central maxima is obtained when `Deltaphi=0`
`kd sin alpha+kd sin theta+kb(1-n)=0`
`sintheta=(b(n-1))/(d)-sinalpha=(1)/(2)rArr` therefore `theta=30^(@)`
At `C`, `theta=0`
`Deltaphi=kd sin alpha-k b (n-1)=(kd)/(2)[1-(2b)/(d)(n-1)]`
`=(2pid)/(2lambda)[1-(2b)/(d)(n-1)]`
Substituting the values, we get, `Deltaphi= -100 pi=2m pi rArr m= -50`
As `I prop cos^(2)((Deltaphi)/(2))`
Hence at `C` there will be maxima.
For minima
`Deltaphi=(2m-1)pi`
for `m= -50` and `-49`, we get `Deltaphi= -101pi` and `-99pi`, respectively.
Hence the minima closest to `theta=0` are of order `m=-49` and `-50` on both side
The phase difference at `C` when we remove the slab
`Deltaphi=100pi` i.e. `m=50`
Hence number of frings passed over `=150`
Promotional Banner

Topper's Solved these Questions

  • OPTICS

    FIITJEE|Exercise Illustration|10 Videos

  • OPTICS

    FIITJEE|Exercise SOLVED PROBLEMS (SUBJECTIVE)|18 Videos

  • MODERN PHYSICS

    FIITJEE|Exercise Numerical based questions|5 Videos

  • PHYSICS PART-III

    FIITJEE|Exercise NUMERICAL BASED QUESTIONS DECIMAL TYPE|11 Videos

Similar Questions

Explore conceptually related problems

In a Young's double slit experiment (slit distance d) monochromatic light of wavelength lambda is used and the figure pattern observed at a distance L from the slits. The angular position of the bright fringes are

In a Young's double slit experiment, (slit distance d) monochromatic light of wavelength lambda is used and the fringe pattern observed at a distance D from the slits. The angular position of the bright fringes are

Two slits in YDSE are placed 1 mm from each other. Interference pattern is observed on a screen placed 1m from the plane of slits. What is the angular fringe width for a light of wavelength 400 nm

In Young's double slit experiment the two slits are d distance apart. Interference pattern is observed on a screen at a distance D from the slits. A dark fringe is observed on the screen directly opposite to one of the slits. The wavelength of light is

Two slits in YDSE are placed 2 millimeter from each other. Interference pattern is observed on a screen placed 2m from the plane of slits. What is the fringe width for a light of wavelength 400 nm ?

A monochromatic light of lambda = 500 Å is incident on two indentical slits separated by a distance of 5 xx 10^(-4) m. The interference pattern is seen on a screen placed at a distance of 1 m from the plane of slits. A thin glass plate of thickness 1.5 xx 10^(-6) m and refractive index mu = 1.5 is placed between one of the slits and the screen . Find the intensity at the center of the screen.

Two slits in YDSE are placed 2 millimetre from each other. Interference pattern is observedon a screen placed 2 m from the plane of slits. What is the fringe width for a light of wavelength 400 nm?

Light of wavelength lambda=5000Å falls normally on a narrow slit. A screen is placed at a distance of 1m from the slit and perpendicular to the direction of light. The first minima of the diffraction pattern is situated at 5mm from the centre of central maximum. The width of the slit is

A YDSE is performed in a medium of refractive index 4 // 3 , A light of 600 nm wavelength is falling on the slits having 0.45 nm separation . The lower slit S_(2) is covered b a thin glass plate of thickness 10.4 mm and refractive index 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown in figure. (All the wavelengths in this problem are for the given medium of refractive index 4 // 3 , ignore absorption.) Find the light intensity at point O relative t maximum fringe intensity.

A beam of light of wavelength 400 nm falls on a narrow slit and the resulting diffraction pattern is observed on a screen 2 m away from the slit. It is observed that 2nd order minima occurs at a distance of 2 mm from the position of central maxima. Find the width of hte slit.