Home
Class 12
CHEMISTRY
P(1),P(2),P(3),are:...


`P_(1),P_(2),P_(3),are:`

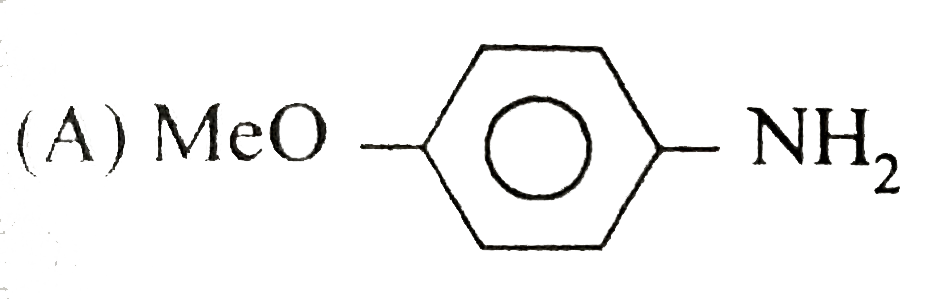
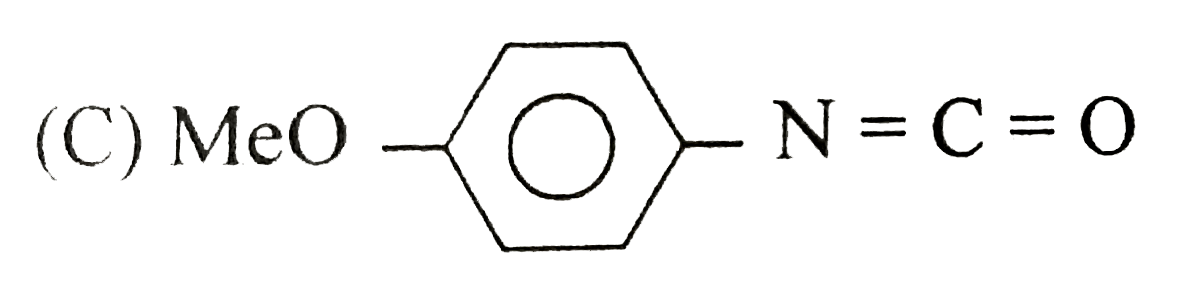
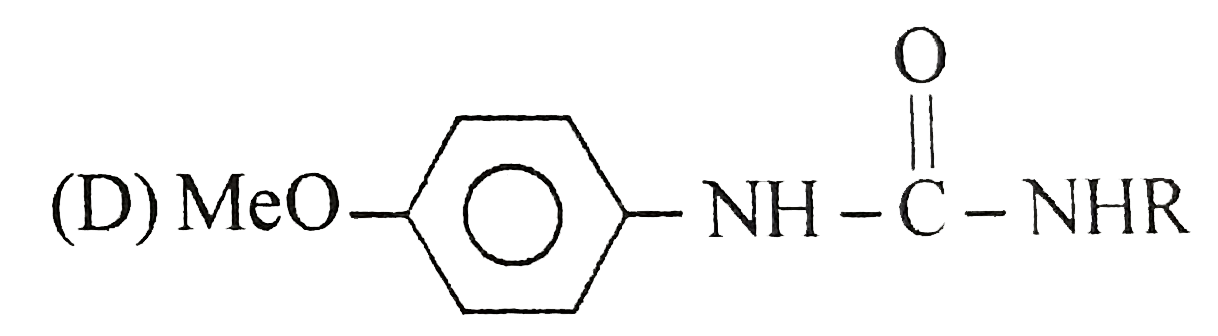
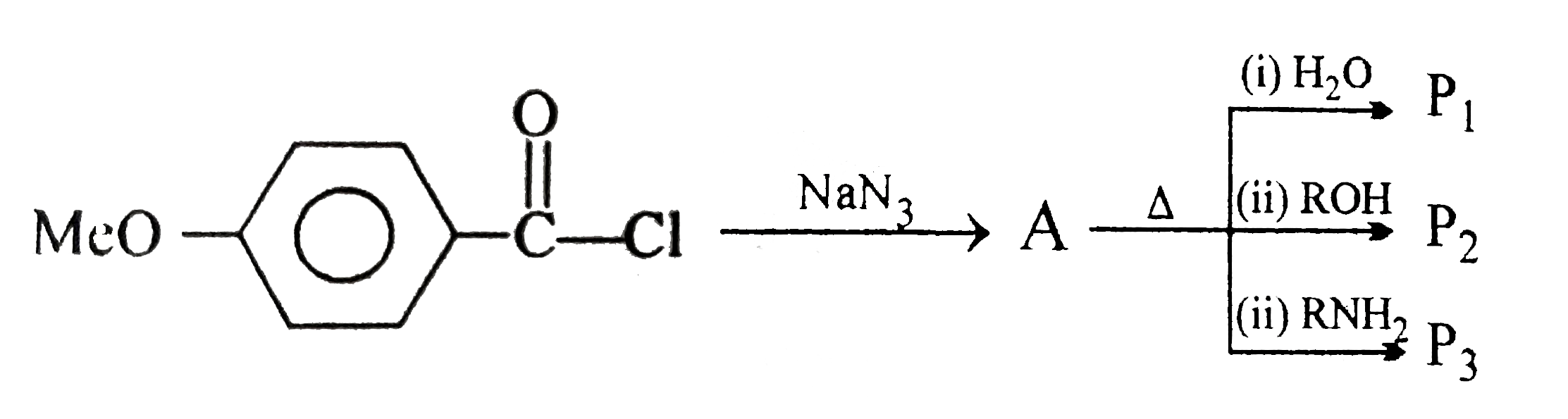A

B

C

D

Text Solution

Verified by Experts

The correct Answer is:
A, B, D
Promotional Banner

Topper's Solved these Questions

  • NITROGEN COMPOUNDS

    BANSAL|Exercise EXERCISE- 2 MATCH THE COLUMN|3 Videos

  • NITROGEN COMPOUNDS

    BANSAL|Exercise EXERCISE-3 (Miscellaneous Exercise)|8 Videos

  • NITROGEN COMPOUNDS

    BANSAL|Exercise EXERCISE-2 Reasoning Type|3 Videos

  • GENERAL ORGANIC CHEMISTRY

    BANSAL|Exercise Exercise 3|19 Videos

  • P BLOCK ELEMENTS

    BANSAL|Exercise Exercise 3|20 Videos

Similar Questions

Explore conceptually related problems

If the length of the perpendicular from the vertices of a triangle A,B,C on the opposite sides are P_(1),P_(2),P_(3) then (1)/(P_(1))+(1)/(P_(2))+(1)/(P_(3))=

IF P_(1),P_(2),P_(3),P_(4) are points in a plane or space and O is the origin of vectors,show that P_(4) coincides with Oiff vec OP_(1)+vec P_(1)P_(2)+vec P_(2)P_(3)+vec P_(3)P_(4)=vec 0

Sixteen players P_(1),P_(2),P_(3)….., P_(16) play in tournament. If they grouped into eight pair then the probability that P_(4) and P_(9) are in different groups, is equal to

Tangent at a point P_(1) [other than (0,0)] on the curve y=x^(3) meets the curve again at P_(2) . The tangent at P_(2) meets the curve at P_(3) & so on.Show that the abscissae of P_(1),P_(2),P_(3),.......P_(n), form a GP.Also find the ratio area of A(P_(1)P_(2)P_(3).) area of Delta(P_(2)P_(3)P_(4))

16 players P_(1),P_(2),P_(3),….P_(16) take part in a tennis tournament. Lower suffix player is better than any higher suffix player. These players are to be divided into 4 groups each comprising of 4 players and the best from each group is selected to semifinals. Q. Number of ways in which they can be divided into 4 equal groups if the players P_(1),P_(2),P_(3) and P_(4) are in different groups, is:

If X be a random variable taking values x_(1),x_(2),x_(3),….,x_(n) with probabilities P_(1),P_(2),P_(3) ,….. P_(n) , respectively. Then, Var (x) is equal to …….. .

There are 10 persons named P_(1),P_(2),P_(3)...,P_(10) Out of 10 persons,5 persons are to be arranged in a line such that is each arrangement P_(1) must occur whereas P_(4) and P_(5) do not occur.Find the number of such possible arrangements.

Players P_(1), P_(2), P_(3), P_(4) toss a fair coin one after another independently till a player gets a head. If P_(1) starts the toss, what is the probability that P_(1) will get head first?

Players P_(1),P_(2),P_(3),P_(4) play knock out tournament.It is known that if P_(i), and P_(j) play,then P_(i), will win if i