Home
Class 12
PHYSICS
A small object of uniform density rolls ...

A small object of uniform density rolls up a curved surface with an initial velocity v. it reaches up to a maximum height of `(3v^2)/(4g)`

with respect to the initial position. The object is

A

ring

B

solid sphere

C

hollow sphere

D

disc

Text Solution

Verified by Experts

The correct Answer is:
d
Promotional Banner

Topper's Solved these Questions

  • RE-NEET 2024

    NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE)|Exercise Question|50 Videos

  • SOLID AND SEMICONDUCTOR DEVICES

    NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE)|Exercise Exercise|105 Videos

Similar Questions

Explore conceptually related problems

A small object of uniform density rolls up a curved surface with an initial velocity v . It reached upto maximum height of 3v^(2)//4g with respect to the initial position. The object is - .

A small object of uniform density rolls up a curved surface with an initial velocity 'w'. It reaches up to a maximum height of (3u^(2))/(4g) with respect to initial position. The object is:

A small object of uniform density rolls up a curved surface with an initial velocity v. It reaches up to a maximum height of 5v2 / 6g with respect to the initial position. The object is- О. o ring O solid sphere O hollow sphere o disc

When a body thrown vertically up with an initial velocity vo ,then maximum height reached by the body is

An object of radius R and mass M is rolling horizontally without slipping with speed v . It then rolls up the hill to a maximum height h = (3v^(2))/(4g) . The moment of inertia of the object is ( g = acceleration due to gravity)

For a body thrown vertically up with an initial velocity u ,the maximum height reached by body from the ground is

When a ball is thrown up vertically with velocity v_0 , it reaches a maximum height of h. If one wishes to triple the maximum height then the ball should be thrown with velocity

NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE)-ROTATIONAL MOTION-Exercise
  1. The ratio of the accelerations for a solid sphere (mass m, and radius ...

    Text Solution

    |

  2. A rod PQ of mass M and length L is hinged at end P. The rod is kept ho...

    Text Solution

    |

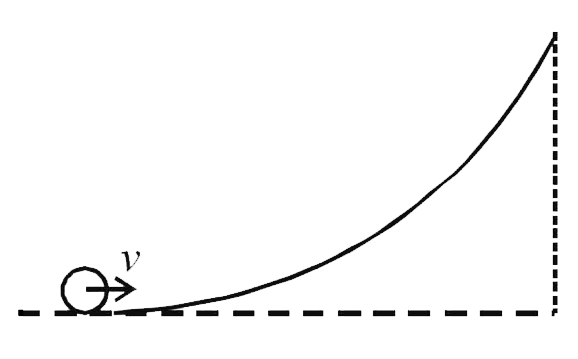
  3. A small object of uniform density rolls up a curved surface with an in...

    Text Solution

    |

  4. When a mass is rotating in a plane about a fixed point, its angular mo...

    Text Solution

    |

  5. Two persons of masses 55 kg and 65 kg respectively are at the opposite...

    Text Solution

    |

  6. O is the centre of an equilateral triangle ABC. F(1), F(2) and F(3) ar...

    Text Solution

    |

  7. A particle moves in a circle of radius 5 cm with constant speed and ti...

    Text Solution

    |

  8. The instantaneous angular position of a point on a rotating wheel is g...

    Text Solution

    |

  9. The moment of inertia of a thin uniform rod of mass M and length L abo...

    Text Solution

    |

  10. A circular disc of moment of inertia I(t) is rotating in a horizontal...

    Text Solution

    |

  11. Two particle which are initially at rest move towards each other under...

    Text Solution

    |

  12. A gramphone record is revolving with an angular velocity omega. A coin...

    Text Solution

    |

  13. Four identical thin rods each of mass M and length l, from a square fr...

    Text Solution

    |

  14. Two bodies of mass 1 kg and 3 kg have position vectors hat i+ 2 hat j ...

    Text Solution

    |

  15. A thin circular ring of mass M and radius R is rotating in a horizonta...

    Text Solution

    |

  16. If vec F is the force acting in a particle having position vector vec ...

    Text Solution

    |

  17. A thin rod of length L and mass M is bent at its midpoint into two hal...

    Text Solution

    |

  18. The ratio of the radii of gyration of a circular disc to that of a cir...

    Text Solution

    |

  19. A particle of mass m moves in the XY plane with a velocity v along the...

    Text Solution

    |

  20. A wheel has angular acceleration of 3.0 rad//s^2 and an initial angula...

    Text Solution

    |