Home
Class 12
PHYSICS
A rod of weight w is supported by two pa...

A rod of weight w is supported by two parallel knife edges A and B and is in equilibrium in a horizontal position. The knives are at a distance d from each other. The centre of mass of the rod is at distance x from A. The normal reaction on A is.. And on B is......

A

`(w x)/(d)`

B

`(w d)/(x)`

C

`(w(d-x))/(x)`

D

`(w(d-x))/(d)`

Text Solution

Verified by Experts

As the weight w balances the normal reaction.

So, `w = N_(1) + N_(2)` ...(i)
Now balancing torque about the COM,
i.e., anti-clockwise momentum
= clockwise momentum
`rArr N_(1)x = N_(2)(d-x)`
Putting the value of `N_(2)` from Eq. (i), we get
`N_(1)x = (w-N_(1))(d-x)`
`rArr N_(1)x = wd-wx -N_(1)d + N_(1)x`
`rArr N_(1)D = w(d-x)`
`rArr N_(1) = (w(d-x))/(d)`
Promotional Banner

Topper's Solved these Questions

  • PHYSICAL WORLD AND MEASUREMENT

    NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE)|Exercise Physical|41 Videos

  • RE-NEET 2020

    NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE)|Exercise All Questions|45 Videos

Similar Questions

Explore conceptually related problems

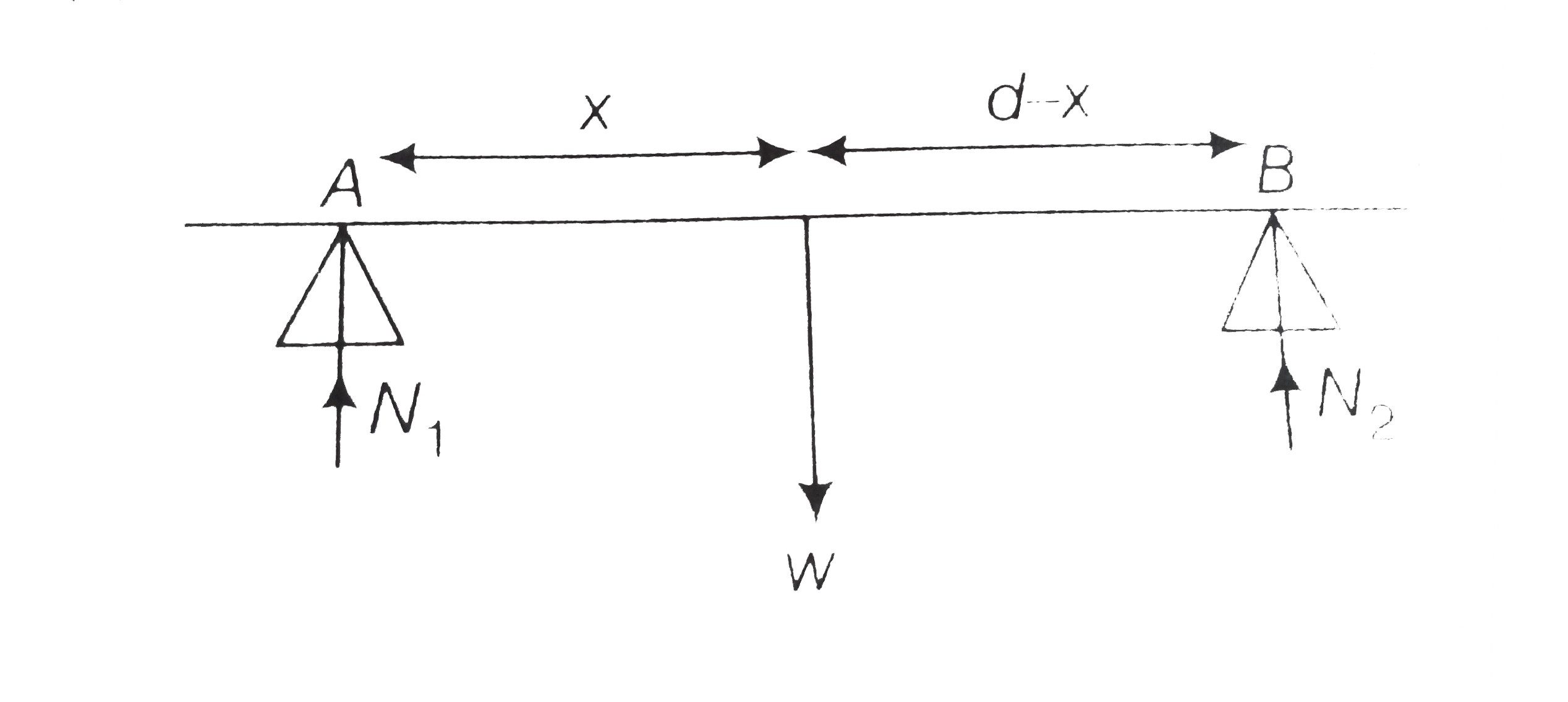
A rod of weight w is supported by two parallel knife edges A and B and is in equilibrium in a horizontal position. The knives are at a distance d from each other. The centre of mass of the rod is at a distance x from A .

A uniform metre rod is bent into L shape with the bent arms at 90^@ to each other. The distance of the centre of mass from the bent point is

A uniform rod AB hinged about a fixed point P is initially vertical. A rod is released from vertical position. When rod is in horizontal position: The acceleration of the centre of mass of the rod is

A rod of length 3m and its mass par unit length is directly proportional to the distance x from its one end . The centre of gravity of the rod from that end will be at :-

A uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity omega about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is

A uniform rod o length one meter is bent at its midpoint to make 90^@ . The distance of centre of mass from the centre of rod is (in cm )

A uniform rod of mass m , length l rests on a smooth horizontal surface. Rod is given a sharp horizontal impulse p perpendicular to the rod at a distance l//4 from the centre. The angular velocity of the rod will be

A uniform rod of mass m and length L lies radialy on a disc rotating with angular speed omega in a horizontal plane about vertical axis passing thorugh centre of disc. The rod does not slip on the disc and the centre of the rod is at a distance 2L from the centre of the disc. them the kinetic energy of the rod is

A uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse J is applied to the end B , perpendicular to the rod in the horizontal direction. Speed of particlem P at a distance (l)/(6) from the centre towards A of the rod after time t = (pi m l)/(12 J) is.