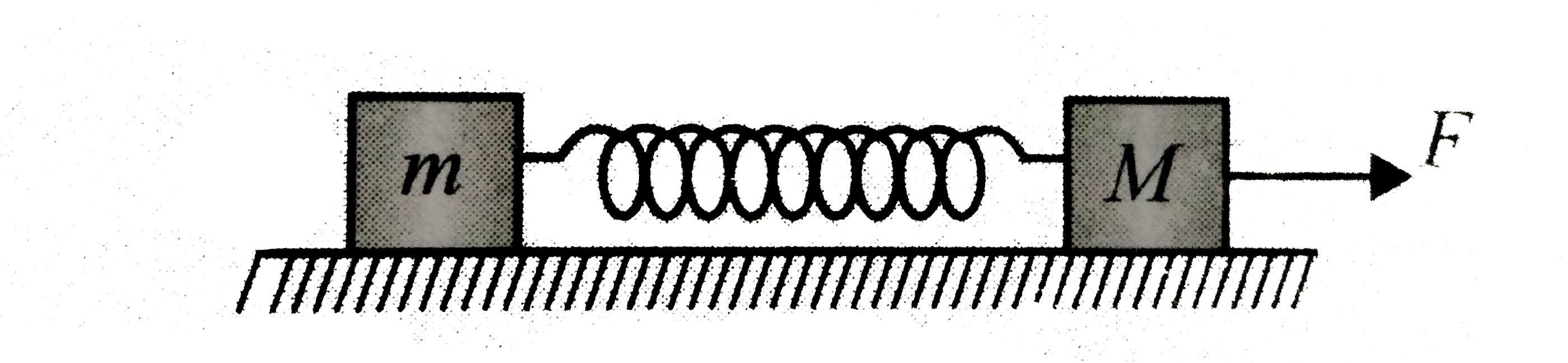Text Solution
Verified by Experts
Topper's Solved these Questions
CENTRE OF MASS & MOMENTUM CONSERVATION
BANSAL|Exercise Practice Exercise|20 VideosCENTRE OF MASS & MOMENTUM CONSERVATION
BANSAL|Exercise EXERCISE-1 [SINGLE CORRECT CHOICE TYPE]|23 VideosCENTRE OF MASS & MOMENTUM CONSERVATION
BANSAL|Exercise EXERCISE-4 (SECTION-B) (JEE-ADVANCED Previous Year Questions)|8 VideosGRAVITATION
BANSAL|Exercise EXERCISE -4 Section - B|6 Videos
Similar Questions
Explore conceptually related problems
BANSAL-CENTRE OF MASS & MOMENTUM CONSERVATION-Solved Examples
- A square hole is punched out of a circular lamina, the diagonal of the...
Text Solution
|
- Find out the centre of mass of a composite object shown in figure. Obj...
Text Solution
|
- For the figure shown, block of mass m is released from the rest. Find ...
Text Solution
|
- Two identical blocks A and B , each of mass m resting on smooth floor ...
Text Solution
|
- A 20 g bullet pierces through a plate of mass M(1) = 1 kg and then com...
Text Solution
|
- A block of mass 4kg is moving with a velocity of 7m//s on a surface. I...
Text Solution
|
- A particle of mass'm' is projected with velocity v(0) at an angle 'alp...
Text Solution
|
- After falling from rest through a height h a body of mass m begins to ...
Text Solution
|
- A block of mass m is connected to another block of mass M by a massles...
Text Solution
|
- A glass ball collides with a smooth horizontal surface (xz plane) with...
Text Solution
|
- A stationary body explodes into four identical fragments such that thr...
Text Solution
|
- A man of mass m climbs to a rope ladder suspended below a balloon of m...
Text Solution
|
- A particle of mass m strikes elastically with a disc of radius R, with...
Text Solution
|
- A wedge mass m rest on horizontal surface. The inclination of the wedg...
Text Solution
|
- A missile of M moving with velocity v=200m//s explodes in midair break...
Text Solution
|