Similar Questions
Explore conceptually related problems
Recommended Questions
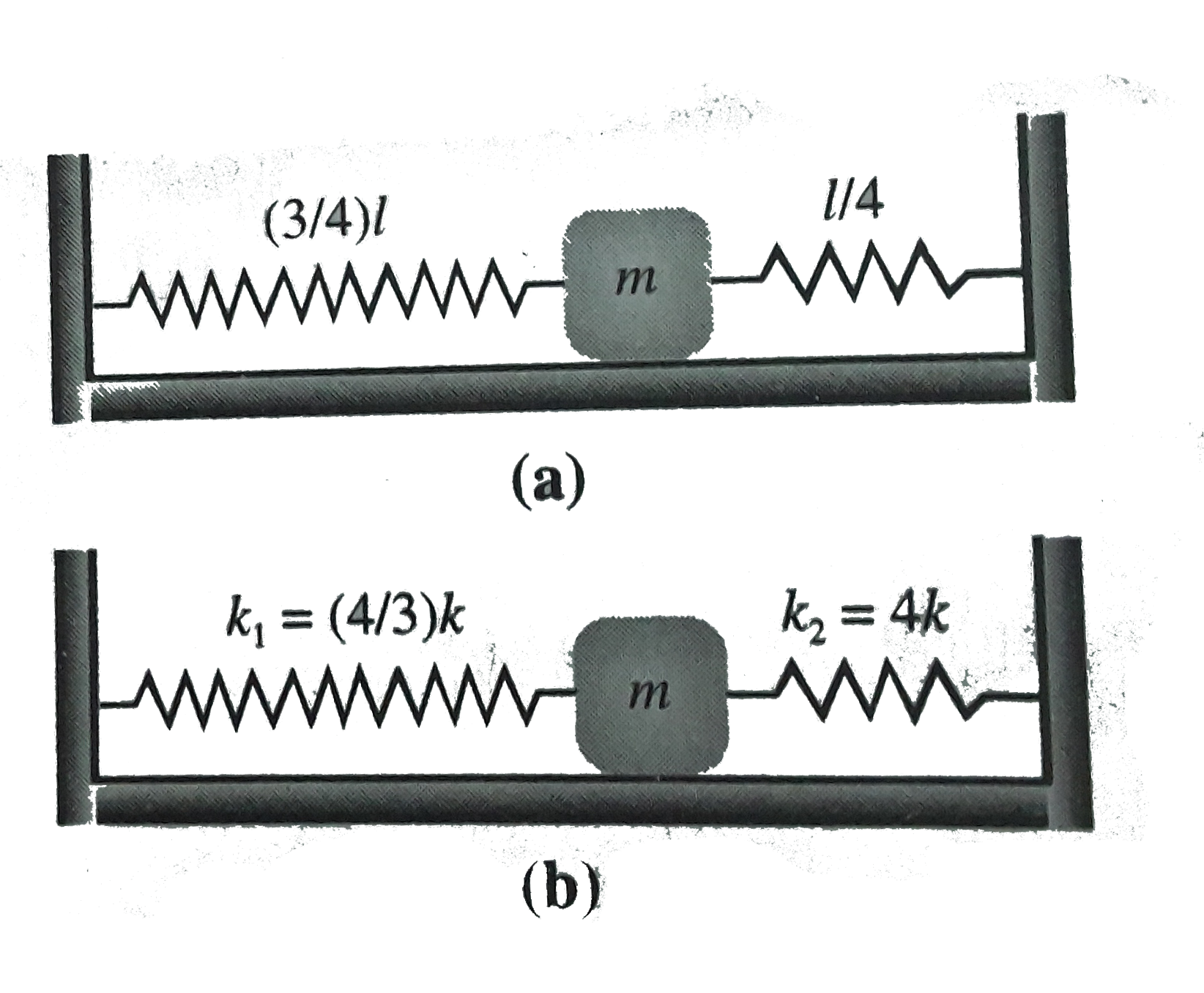
- A spring of stiffness constant k and natural length l is cut into two ...
Text Solution
|
- A spring of stiffness constant k and natural length l is cut into two ...
Text Solution
|
- If a spring of stiffness 'k' is cut into two parts 'A' and 'B' of leng...
Text Solution
|
- A body of mass m is suspended from three springs as shown in figure. I...
Text Solution
|
- A mass m performs oscillations of period T when hanged by spring of fo...
Text Solution
|
- In a spring- mass system , the length of the spring is L, and it has a...
Text Solution
|
- लम्बाई l तथा द्रव्यमान m के गोलक से बने हुआ एक सरल लोलक का दोलन-अवधि ...
Text Solution
|
- A body of mass 'm' hangs from three springs, each of spring constant '...
Text Solution
|
- A mass suspended from a spring of spring constant k is made to oscilla...
Text Solution
|