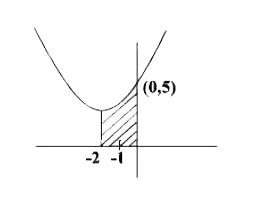
The area bounded by the curve y = x^2 + ...

The area bounded by the curve `y = x^2 + 4x + 5`, the axes of co-ordinates & the minimum ordinate is:

A

`3 2/3` sq. unit

B

`4 2/3` sq. unit

C

`5 2/3` sq. unit

D

`8/3` sq. unit

Verified by Experts

The correct Answer is:

B

`y =x^(2)+4x+5=(x+2)^(2)+1`
`A = int_(-2)^(0)(x^(2)+4x+5)dx=(x^3)/(3)+2x^(2)+5 ]_(2)^(0)`

`-[-8/3+8-10] = 2+8/3=14/3=4 2/3`.

Similar Questions

Explore conceptually related problems

Calculate the area bounded by the curve y=x(3-x)^(2) the x-axis and the ordinates of the maximum and minimum points of the curve.

The area bounded by the curve y=(4)/(x^(2)) , x -axis and the ordinates x=1,x=3 is

The area bounded by the curve y = log x, X- axis and the ordinates x = 1, x = 2 is

Find the area bounded by the curve y=log xx -axis and the ordinates x=18x=e

Find the area bounded by the curve y=4x-x^2 , the x-axis and the ordinates x=1 and x=3 .

Area bounded by the curve y = x ^(2), the x-axis and the ordinates x =-2 and x =1 is :

The area bounded by the curve y=x|x| , x-axis and the ordinates x=1,x=-1 is given by

Find the area bounded by the curve y=x|x| , x-axis and ordinates x=-1 and x=1 .