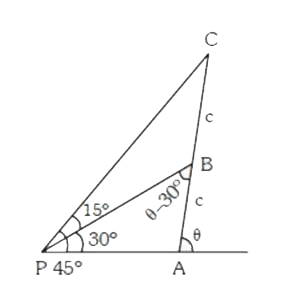
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A man observes that when he moves up a distance c metres on a slope, t...
Text Solution
|
- A person in a balloon, who has ascended vertically from flat land at t...
Text Solution
|
- A man from the top of a 100 metres high tower sees a car moving toward...
Text Solution
|
- The angle of depression of a point situated at a distance of 70 metres...
Text Solution
|
- The angle of elevation of the top of a hill from a point on the horizo...
Text Solution
|
- A man from the top of a 100 metres high tower observes a car moving to...
Text Solution
|
- Angle of elevation of mountain peak from a point alpha Is horizontal b...
Text Solution
|
- A man from the top of 100 metres high tower sees a car moving towords ...
Text Solution
|
- A person in aballoon, who has ascended verticallly from flat land at t...
Text Solution
|