A
B
C
D
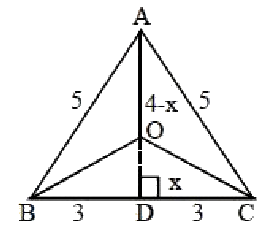
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The bottom of the legs of a three legged table are the vertices of an ...
Text Solution
|
- If the two legs of a right angled triangle are equal and the square of...
Text Solution
|
- The bottom of the legs of a three legged table are the vertices of an ...
Text Solution
|
- One of the legs of a right triangle is 9cm. If the area of the triangl...
Text Solution
|
- The hypotenuse of a right triangle is 3sqrt(10)c m . If the smaller...
Text Solution
|
- The two legs of a right triangle are equal and the square of the hy...
Text Solution
|
- The bottom of the legs of a three legged table are the vertices of an ...
Text Solution
|
- One leg of a right triangle is 1 cm shorter than the other leg and the...
Text Solution
|
- Which three-dimensional figure is formed by rotating a right triangle ...
Text Solution
|