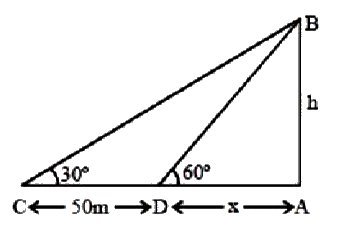
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The angle of elevation of top of a chimney from a point on ground is 3...
Text Solution
|
- The angle of elevation of the top of a chimney from the top of a tower...
Text Solution
|
- 1.5 m लंबा एक प्रेक्षक एक चिमनी से 28 .5 m की दुरी पर है l उसक...
Text Solution
|
- An observer 1.5 m tall is 30 m away from a chimney. The angle of ele...
Text Solution
|
- एक चिमनी के शीर्ष से एक स्तम्भ के शीर्ष का उन्नयन कोण 60^(@) हो जाता ह...
Text Solution
|
- If the angle of elevation of the top of a chimney from a point on the ...
Text Solution
|
- When the top of a chimney of a factory is seen from a point on the roo...
Text Solution
|
- Form a point on the same plane along the horizontal line passes throug...
Text Solution
|
- The angle of elevation of the top of a chimney at a distance of 200 m ...
Text Solution
|