A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
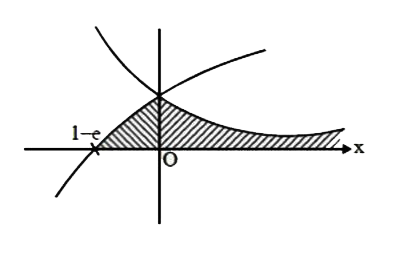
- Find the area enclosed between the curves: y = loge (x + e) , x = loge...
Text Solution
|
- Find the area enclosed between the curves: y=log(e)(x+e),x=log(e)((1)/...
Text Solution
|
- Find the area enclosed by the graph of y=log(e)(x+1),y-axis, and the l...
Text Solution
|
- वक्र y=log(e)x, X-अक्ष तथा कोटियों x = 1 तथा x = e से घिरे क्षेत्र का ...
Text Solution
|
- वक्र y =log(e ) x,x-अक्ष तथा कोटि x = e द्वारा परिबद्ध क्षेत्रफल है :
Text Solution
|
- वक्र y=log(e)(x+e) तथा अक्षों से परिबद्ध क्षेत्रफल का मान है
Text Solution
|
- The area enclosed between the curve y=loge(x+e) and the coordinate axe...
Text Solution
|
- Find the area enclosed by y=log(e)(x+e) and x=log(e)((1)/(y)) and the ...
Text Solution
|
- The area encosed between the curves y=log(e)(x+e),y=e^(x) and the X-ax...
Text Solution
|