Home
Class 12
MATHS
If maximum & minimum value of function f...

If maximum & minimum value of function `f(x)=x^(3)-6x^(2)+9x+1 AA x in [0, 2]` are M & m respectively, then value of `M – 2m` is :

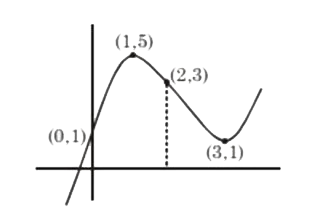
Text Solution

Verified by Experts

The correct Answer is:
`3.00`

`therefore M = 5` and m = 1
`M - 2m = 3`
Promotional Banner

Similar Questions

Explore conceptually related problems

Minimum value of f(x)=6x^(3) -9x^(2)-36x+24 is

Find the maximum and minimum values of the function y=4x^3-3x^2-6x+1

The minimum value of the function f(x)=(tanx)/(3+2tanx), AA x in [0, (pi)/(2)) is

For x in[1,16],M and m denotes maximum and minimum values of f(x)=log_(2)^(2)x-log_(2)x^(3)+3 respectively,then value of (2M-4m) is-

Let M and m respectively be the maximum and minimum values of the function f(x) = tan^(-1) (sin x + cos x) " in " [0, (pi)/(2)] . Then the vlaue of tan (M-m) is equal to :

Let minimum and maximum value of y=2x^(3)-15x^(2)-36x+1AA x in[0,3] is m and M. Then

Find the maximum and minimum values of the following functions. f(x)=x^(3)-2x^(2)+x+6

The difference between the maximum and minimum values of the function f(x)=x^(3)-3x+4, AA x in {0, 1] is

Real number x,y satisfies x^(2)+y^(2)=1. If the maximum and minimum value of the expression z=(4-y)/(7-x) are M and m respectively,then find the value (2M+6m)

Let x&y be the real numbers satisfying the equation we are of x^(2)-4x+y^(2)+3=0, If the maximum and minimum values of x^(2)+y^(2) are M&m respectively,then find the numerical value of |M+m|