Home
Class 11
PHYSICS
ABCDEF is a regular hexagon, Fig. 2 (c )...

`ABCDEF` is a regular hexagon, Fig. 2 (c ) .65. What is the value of
` (vec (AB) + vec (AC) + vec (AD) + vec (AE) + vec (AF) ?`
.

A

`vec(AO)`

B

`2vec(AO)`

C

`4vec(AO)`

D

`6vec(AO)`

Text Solution

Verified by Experts

The correct Answer is:
D
Promotional Banner

Topper's Solved these Questions

  • UNITS, DIMENSION & MEASUREMENTS

    ERRORLESS |Exercise All Questions|333 Videos

  • WAVES AND SOUND

    ERRORLESS |Exercise SET|25 Videos

Similar Questions

Explore conceptually related problems

ABCDEF is a regular hexagon with point O as centre. The value of vec(AB)+vec(AC)+vec(AD)+vec(AE)+vec(AF) is

In a regular hexagon ABCDEF,vec AE

In Fig. ABCDEF is a ragular hexagon. Prove that vec(AB) +vec(AC) +vec(AD) +vec(AE) +vec(AF) = 6 vec(AO) .

If ABCDE is a pentagon, then vec(AB) + vec(AE) + vec(BC) + vec(DC) + vec(ED) + vec(AC) is equal to

ABCD is a parallelogram Fig. 2 (c ) .64. AC and (BD) are its diagonals. Show that (a) vec (AC) +vec (BD) =2 vec (BC) (b) vec (AC) - vec (BD) =2 vec (AB) .

ABCDEF be a regular hexagon in the xy-plane and vec AB=4hat i then vec CD=

ABCDEF is a regular hexagon with centre a the origin such that vec(AB)+vec(EB)+vec(FC)= lamda vec(ED) then lamda = (A) 2 (B) 4 (C) 6 (D) 3

ABCDEF is a regular hexagon.Find the vector vec AB+vec AC+vec AD+vec AE+vec AF in terms of the vector vec AD

In a regular hexagon ABCDEF, prove that vec(AB)+vec(AC)+vec(AD)+vec(AE)+vec(AF)=3vec(AD)

ERRORLESS -VECTORS-Exercise
  1. A vector vec(a) is turned without a change in its length through a sma...

    Text Solution

    |

  2. Find the resultant of the three vectors vec(OA), vec(OB) and vec(OC) s...

    Text Solution

    |

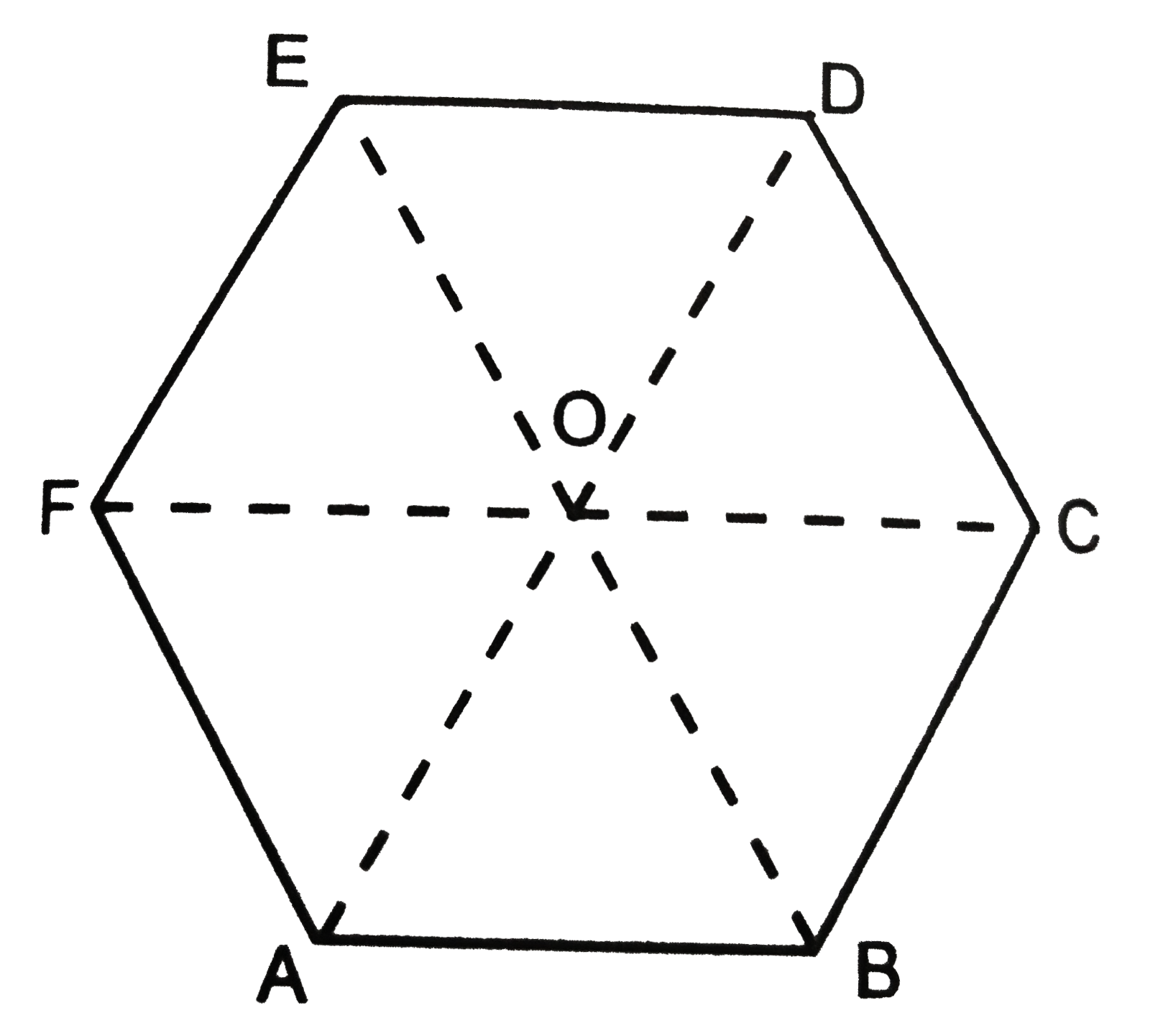
  3. ABCDEF is a regular hexagon, Fig. 2 (c ) .65. What is the value of ...

    Text Solution

    |

  4. The length of second's hand in watch is 1 cm. The change in Velocity o...

    Text Solution

    |

  5. A particle moves towards east with velocity 5m//s. After 10 seconds it...

    Text Solution

    |

  6. A force F=-K(yhati+xhatj) (where K is a positive constant) acts on a p...

    Text Solution

    |

  7. The vectors from origin to the points A and B are vecA=3hati-6hatj+2ha...

    Text Solution

    |

  8. A metal sphere is hung by a string fixed to a wall. The sphere is push...

    Text Solution

    |

  9. A boat having a speed of 5km//hr. in still water, crosses a river of w...

    Text Solution

    |

  10. A man crosses a 320m wide river perpendicular to the current in 4 min....

    Text Solution

    |

  11. Assertion: vecAxxvecB is perpendicular to both vecA+vecB as well as ve...

    Text Solution

    |

  12. Assertion: Angle between hati+hatj and hati is 45^(@). Reason: hati...

    Text Solution

    |

  13. Assertion: If theta be the angle between vecA and vecB then tan theta=...

    Text Solution

    |

  14. Statement-1:If ,|vec A+vec B| =|vecA-vecB| then angle between vecA an...

    Text Solution

    |

  15. Assertion: Vector product of two vectors is an axial vector. Reason:...

    Text Solution

    |

  16. Assertion: Minimum number of non-equal Vectors in a plane required to ...

    Text Solution

    |

  17. Assertion: Relative velocity of A w.r.t B is greater than the velocity...

    Text Solution

    |

  18. Assertion: Vector addition of two vectors vedA and vecB is commutative...

    Text Solution

    |

  19. Assertion: vecA.vecB=vecB.vecA Reason: Dot product of two vectors is...

    Text Solution

    |

  20. Assertion: vectau=vec(r)xxvec(F) and vectau!=vec(F)xxvec(r ) Reason:...

    Text Solution

    |