Home
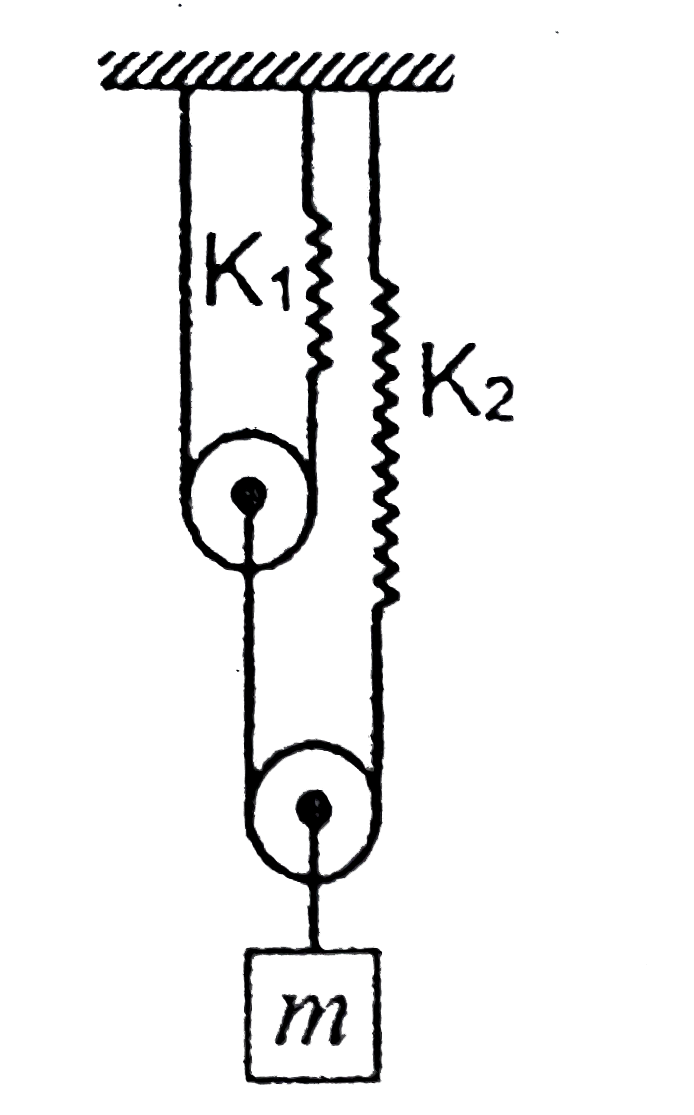
Class 12
PHYSICS
In the given figure pulleys and strings ...

In the given figure pulleys and strings are ideal. The time period of (Assume that string remains taut) vertical oscillations of the block is,

A

`pisqrt((m(K_(2)+4K_(1)))/(K_(1)K_(2)))`

B

`(pi)/2sqrt((m(K_(2)+4K_(1)))/(K_(1)K_(2))`

C

`2pisqrt((m(K_(1)+K_(2)))/(K_(1)K_(2))`

D

none of these

Text Solution

Verified by Experts

The correct Answer is:
B
Suppose extension in two spring are `x_(1)` and `x_(2)`
Displacement of block
`x=(x_(2))/2+(x_(1))/4`
`2K_(1)x_(1)=K_(2)x_(2)=F/2`
`1/(K_(eq))=1/(16K_(1))+1/(4K_(2)),K_(eq)=(16K_(1)K_(2))/(4K_(1)+K_(2))`
`T=2pi sqrt((m(4K_(1)+K_(2)))/(16K_(1)K_(2))),T=(pi)/2 sqrt((m(4K_(1)+K_(2)))/(K_(1) K_(2)))`
Promotional Banner

Similar Questions

Explore conceptually related problems

In the given figure, pulleys and strings are massless. For equilibrium of the system, the value of  is -

In the arrangement shown, the pulleys and the strings are ideal.The acceleration of the block B is

In the given figure, pulleys and strings are massless. For equilibrium of the system, the value of alpha is -

In the shown diagram all pulleys and strings are ideal. The frictional force acting on the 5 block is

In the arrangement shown, the pulleys and the string are ideal. The acceleration of block B is.

There is a system of infinite pulleys and springs.Spring constants are in GP as k 2k 4k 8k.........oo as shown in the figure.All the pulleys are massless frictionless and strings are massless and inextensible.Then time period of small oscillations of the block will be (Mass of block is m ). qquad (in ) (i) 2

In the shown mass pulley system, pulleys and string are massless. The one end of the string is pulled by the force F = mg. The acceleration of the block will be :

In the shown mass pulley system, pulleys and string are massless. The one end of the string is pulleed by the force F=2mg . The acceleration of the block will be

The string, spring and the pulley shown in figure are light. Find the time period of the mass m .