A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
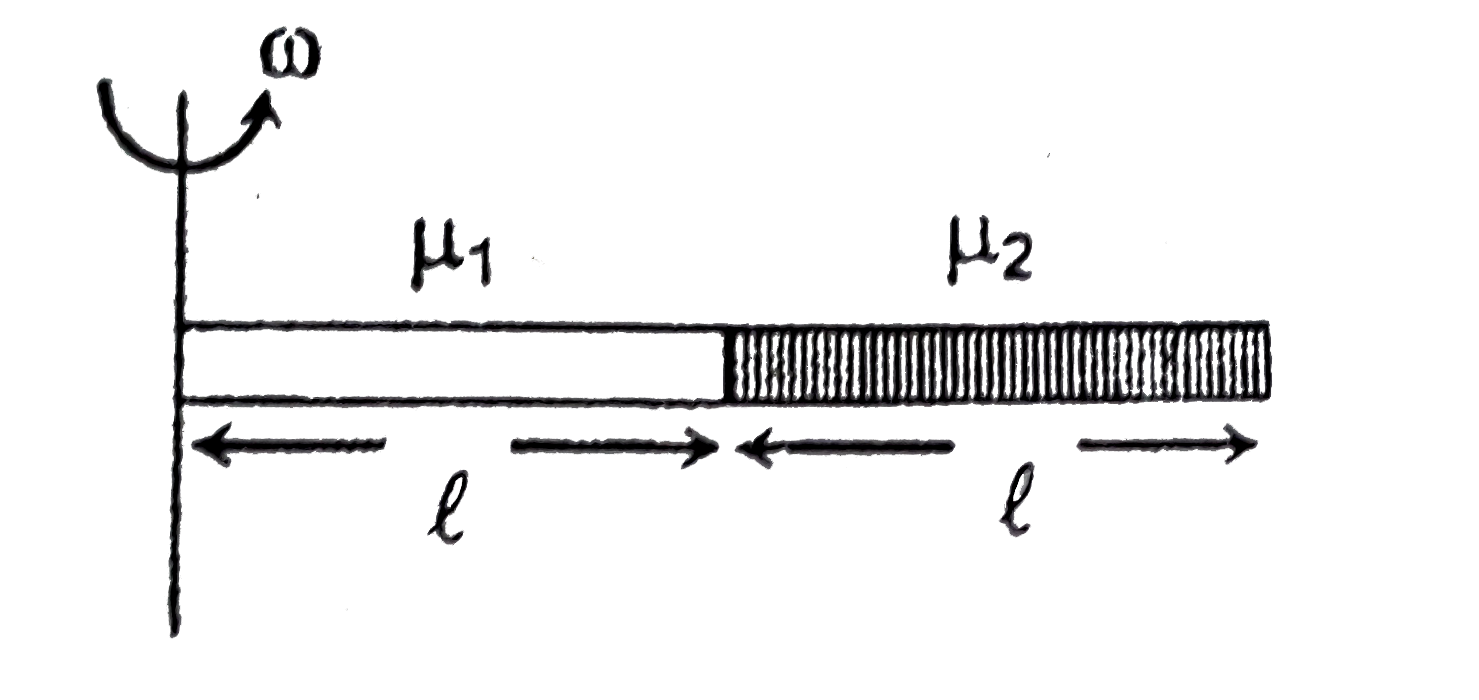
- Two thin rods of same length l but of different uniform mass per unit ...
Text Solution
|
- Two identical thin uniform rods of length L each are joined to form T ...
Text Solution
|
- Two beads of mass 2m and m , connected by a rod of length l and of neg...
Text Solution
|
- A uniform rod of mass m and length L is suspended with two massless st...
Text Solution
|
- Two strings A and B are connected together end to end as shown in the ...
Text Solution
|
- The ratio of I(AA)/I(BB) will be (both are identical thin rods of leng...
Text Solution
|
- Two strings of the same length but different mass per unit length are ...
Text Solution
|
- Two thin rods of same length l but of different uniform mass per unit ...
Text Solution
|
- Consider the situation shown in the figure. Uniform rod of length L ca...
Text Solution
|