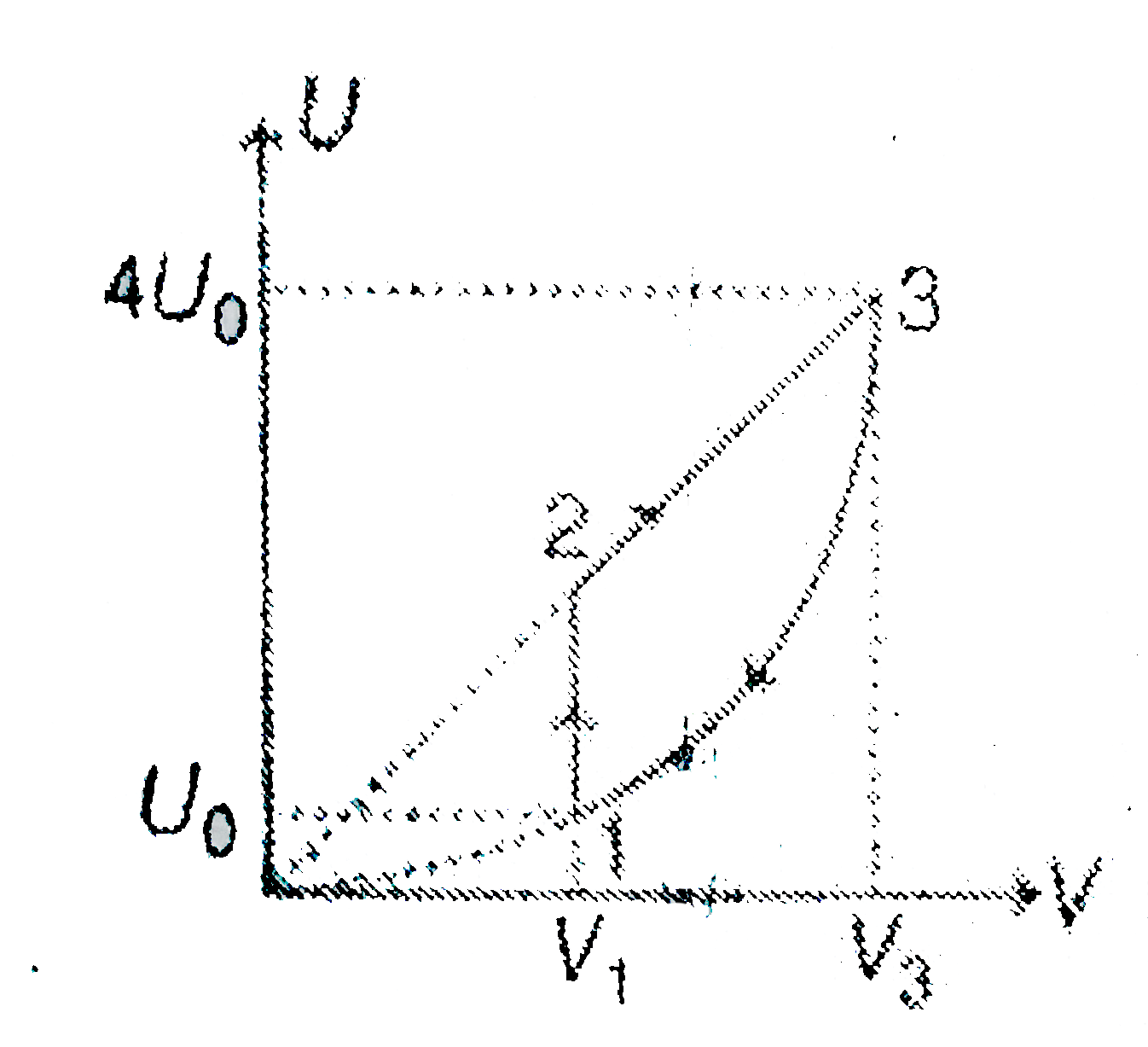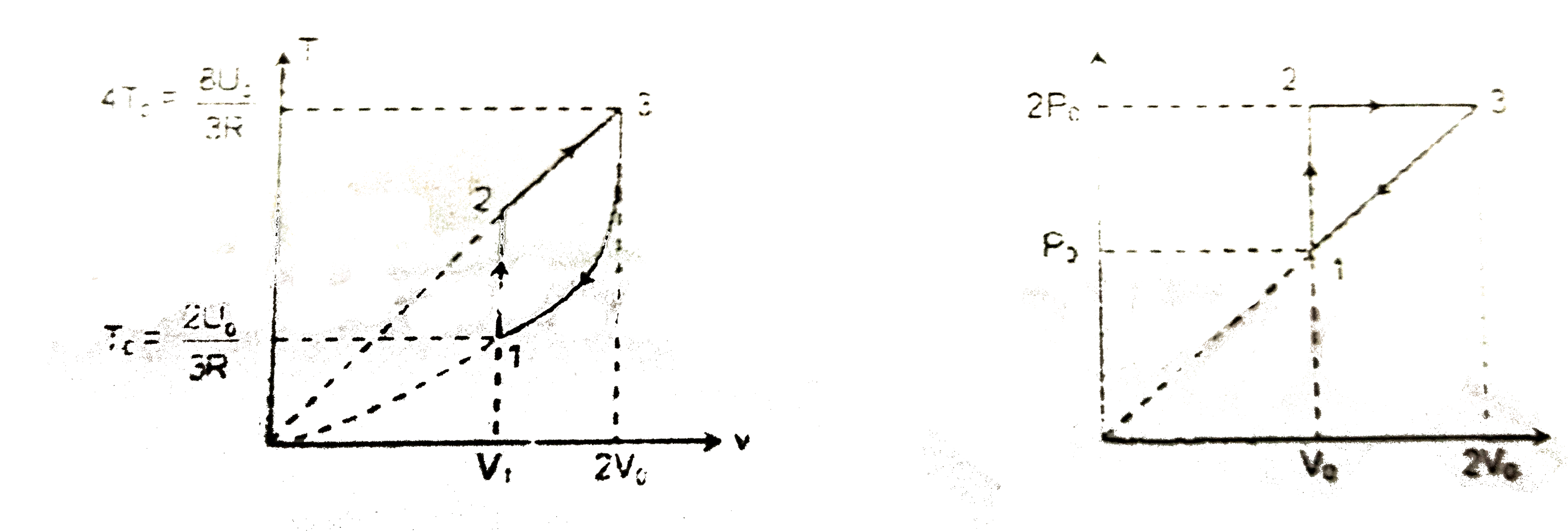A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- One mole of helium gas follows the cycle 1-2-3-1 shown in the diagram....
Text Solution
|
- An ideal gas of mass m in a state A goes to another state B via three ...
Text Solution
|
- Three processes compose a thermodynamic cycle shown in the accompanyin...
Text Solution
|
- An ideal gas goes from State A to state B via three different process ...
Text Solution
|
- Consider PT graph of cyclic process shown in the figure. Maximum press...
Text Solution
|
- One mole of helium gas follow cycle 1-2-3-1 shown in the diagram. Duri...
Text Solution
|
- For an ideal gas four processes are marked as 1,2,3 and 4 on P-V diagr...
Text Solution
|
- One mole of helium gas follows the cycle 1-2-3-1 shown in the diagram....
Text Solution
|
- One mole of helium gas follows the cycle 1-2-3-1 shown in the diagram....
Text Solution
|