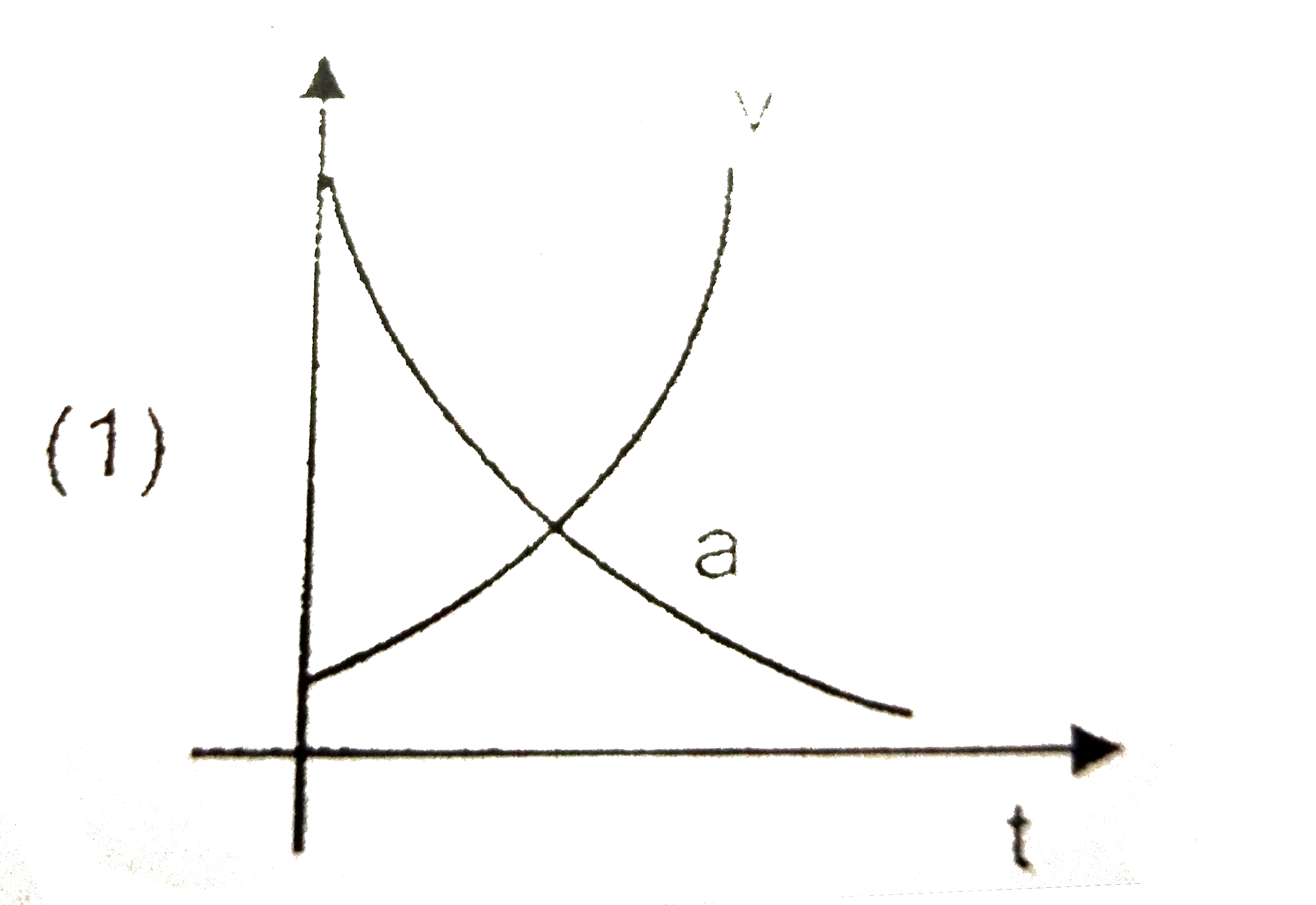
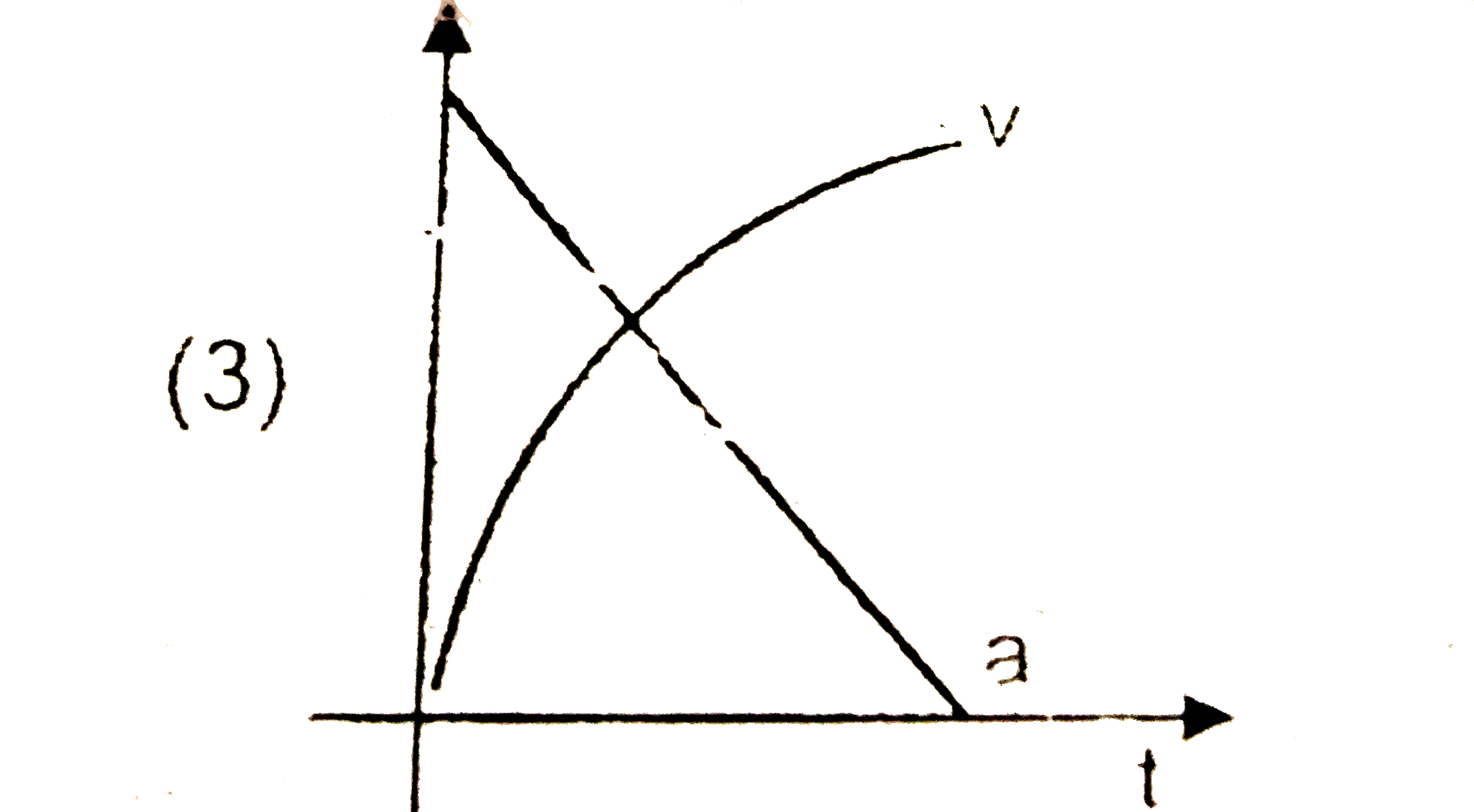
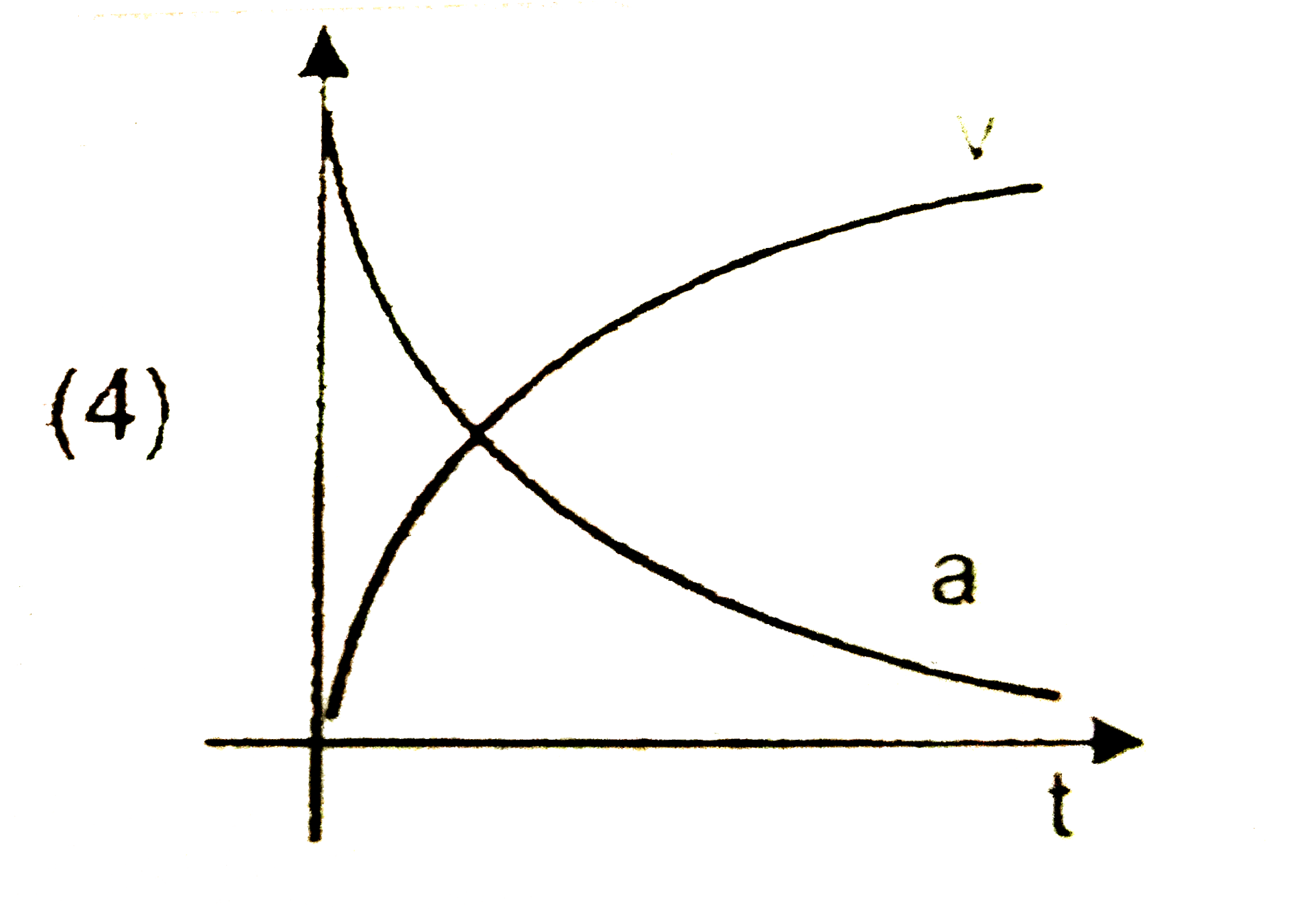
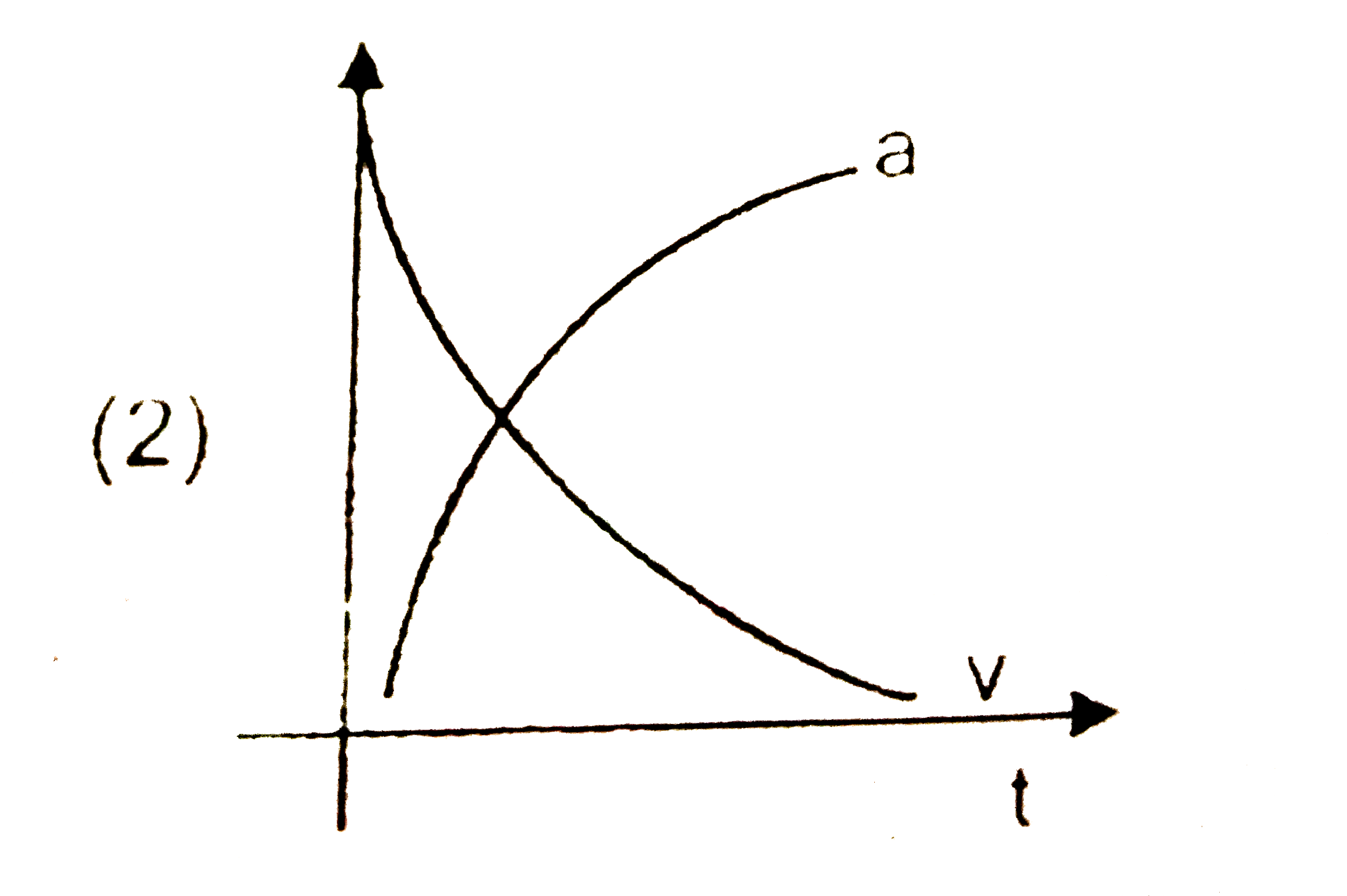A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Which of the following option correctly describes the variation of the...
Text Solution
|
- A small ball (mass m) falling under gravity in a viscous medium experi...
Text Solution
|
- An oil drop of mass m and falls through a medium that offers a viscous...
Text Solution
|
- Which of the following optiona correctly describes the variation of th...
Text Solution
|
- Which of the following option correctly describes the variation of the...
Text Solution
|
- The mass m is placed on a body of mass M. There is no friction. The fo...
Text Solution
|
- In a uniform electric field, a point charge of mass m and charge q is ...
Text Solution
|
- A small point mass carrying some positive charge on it, is released fr...
Text Solution
|
- Two bodies of masses M and 27 M are allowed to fall on a viscous liqui...
Text Solution
|