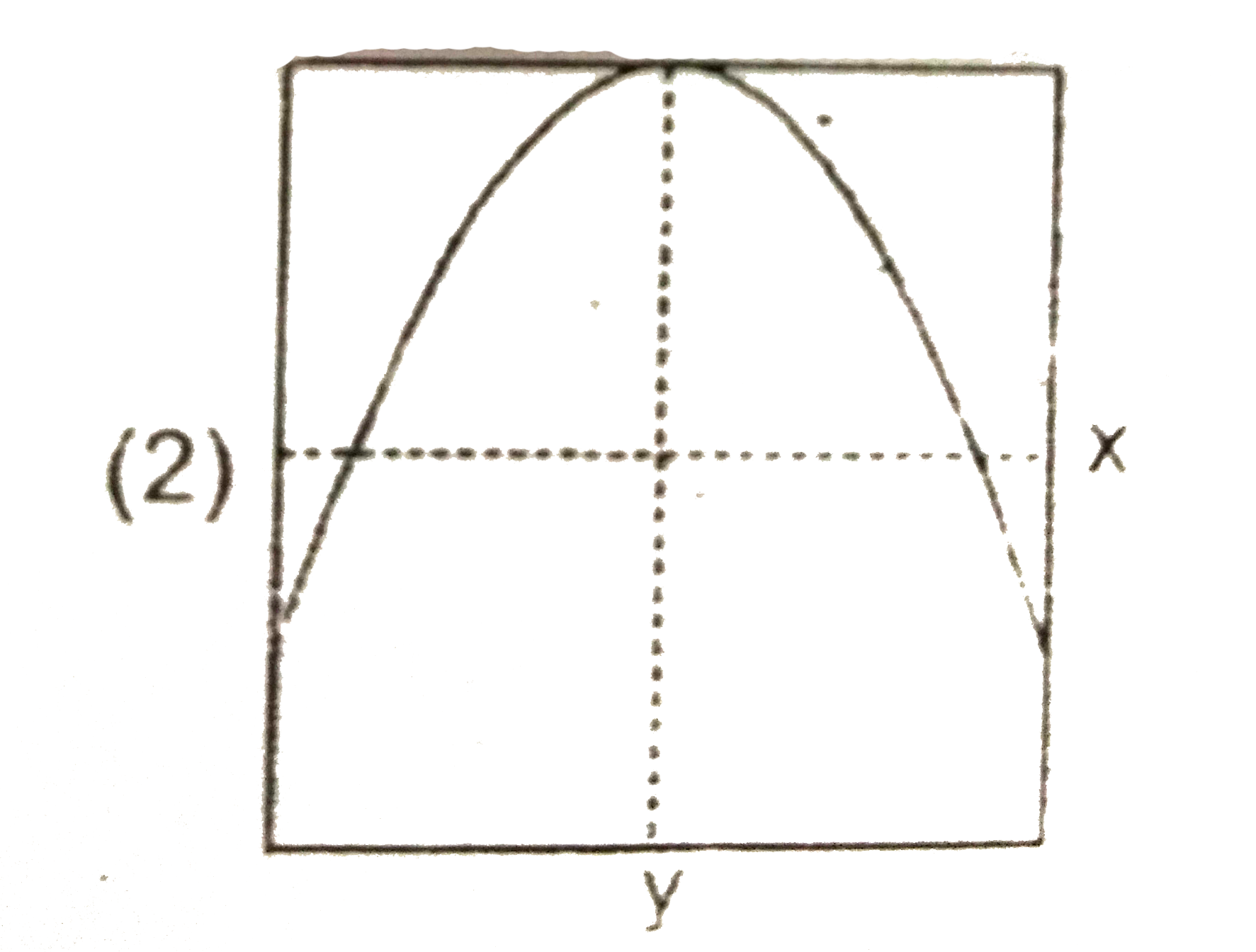
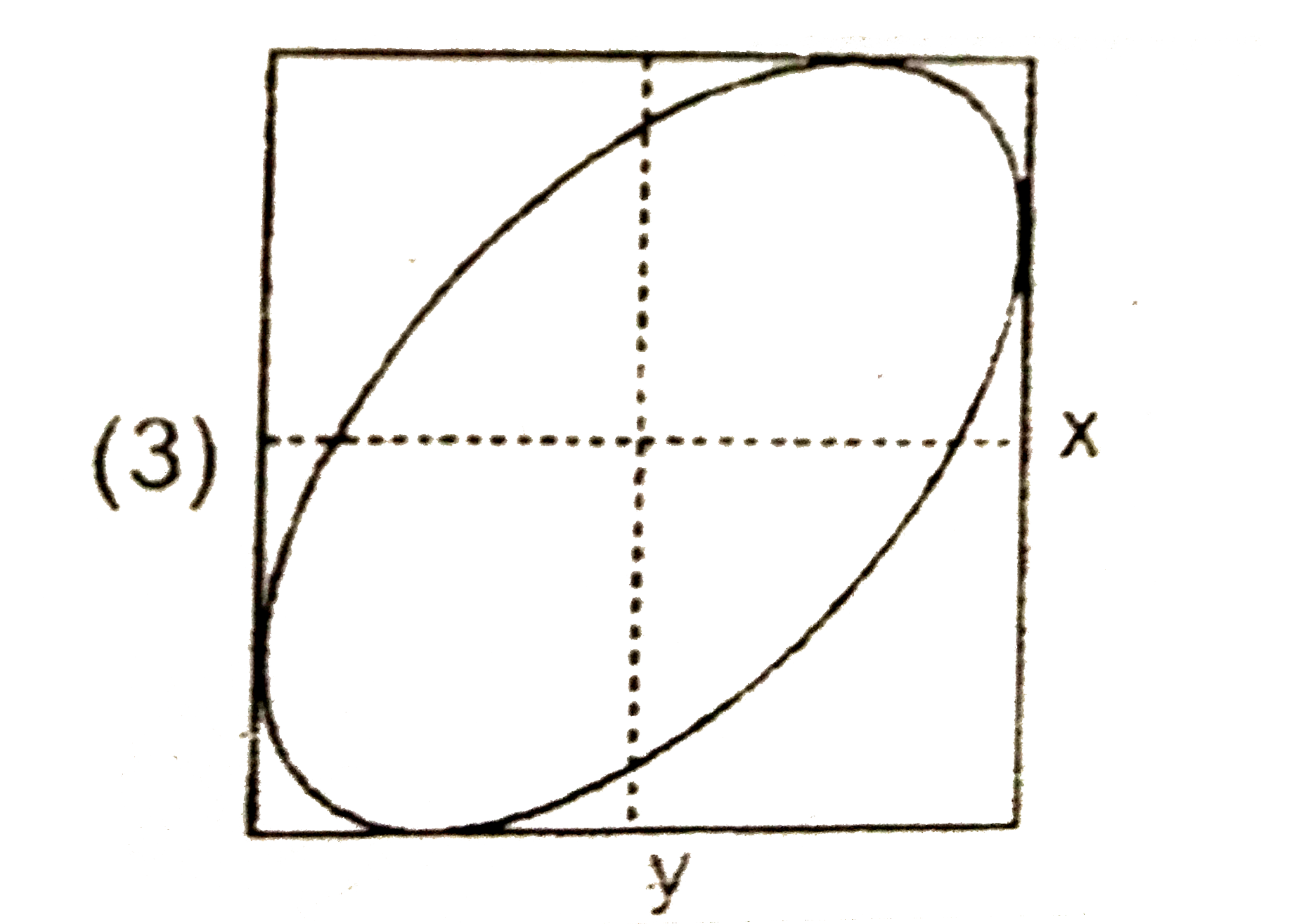
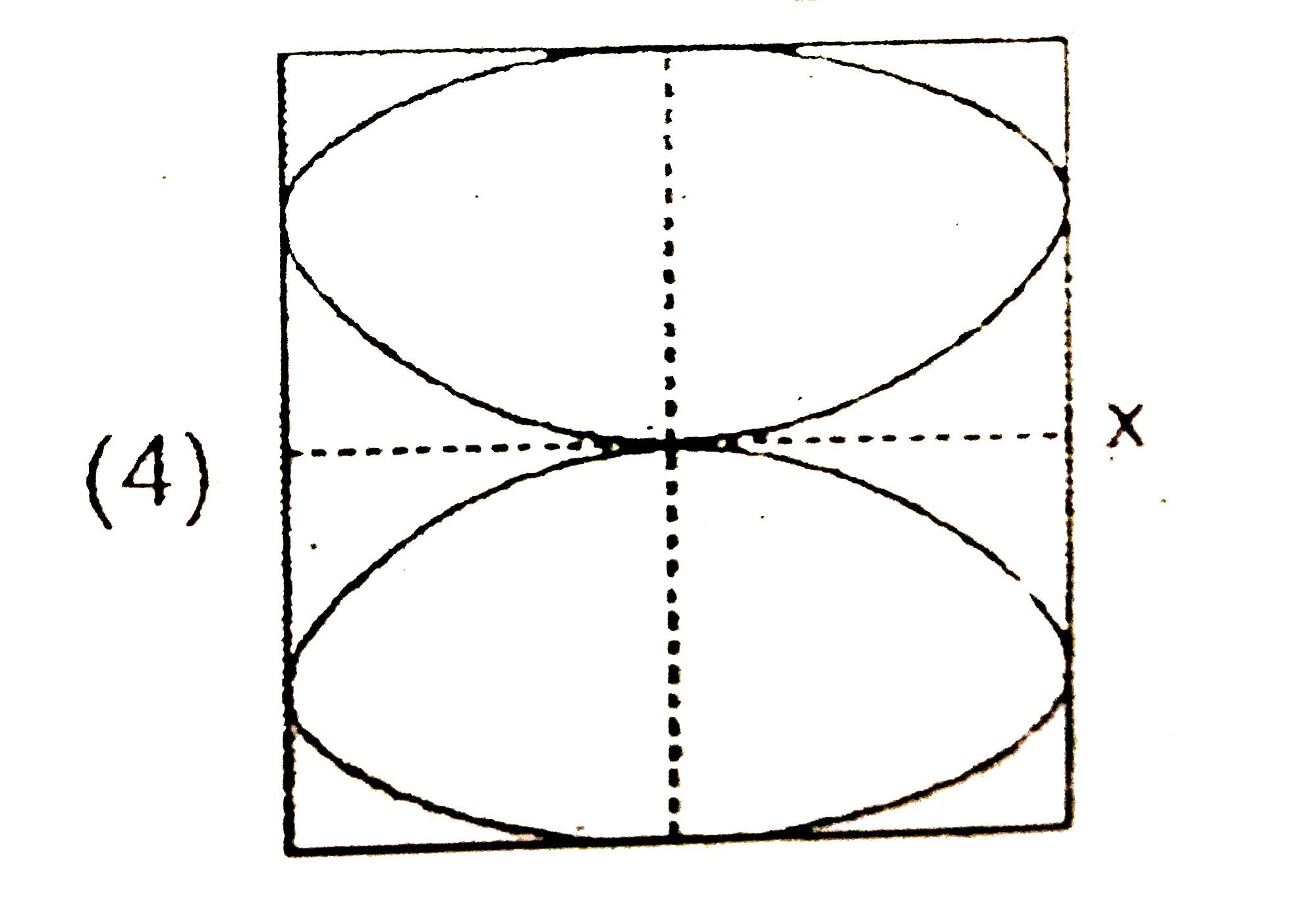
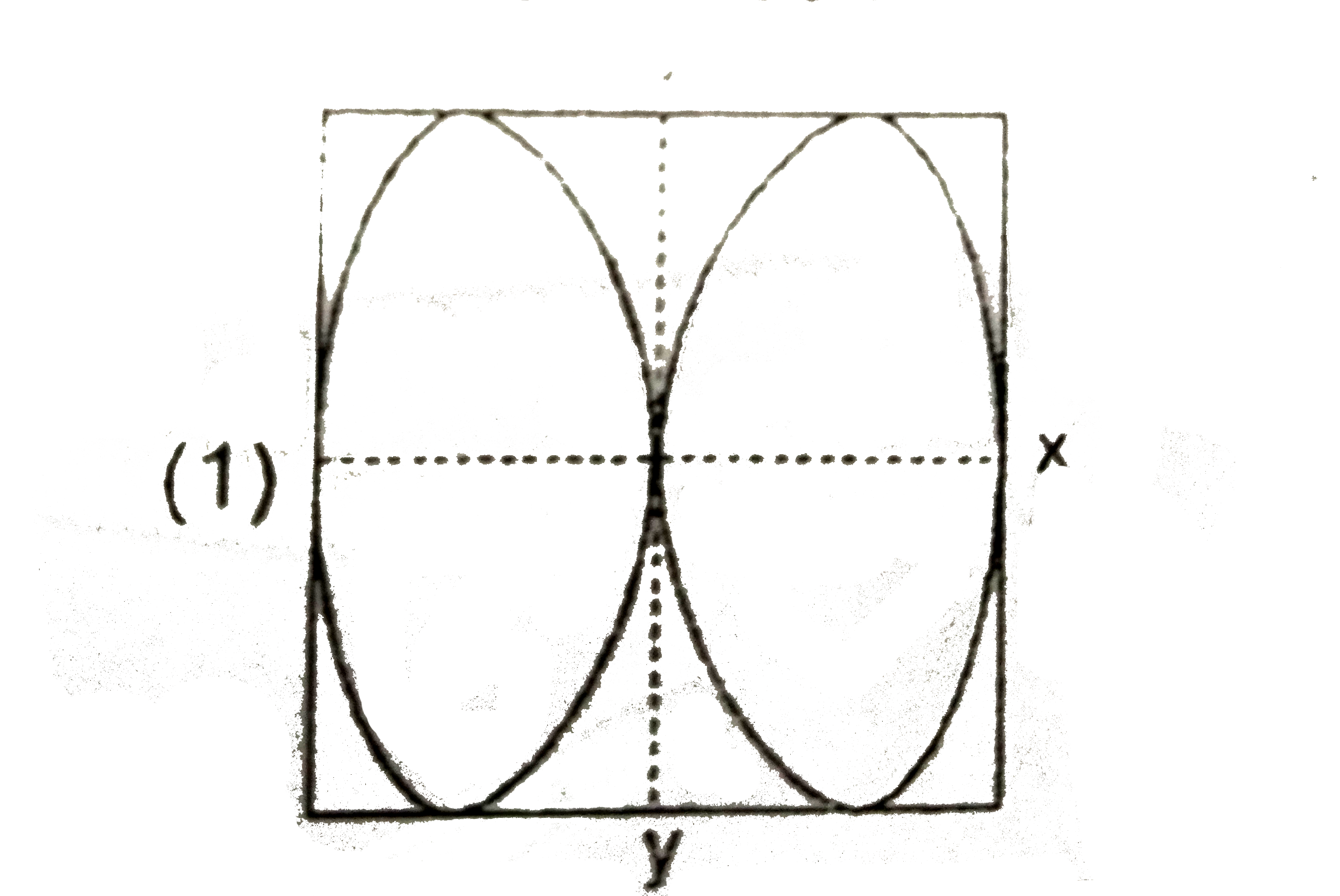A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- x and y displacements of a particle are given as x(t)=-asinomegat and ...
Text Solution
|
- A particle is acted simultaneously by mutually perpendicular simple ho...
Text Solution
|
- x and y displacements of a particle are given as x(t)=-asinomegat and ...
Text Solution
|
- A particle is acted simultaneously by mutally perpendicular simple har...
Text Solution
|
- A particle is acted simultaneously by mutually perpendicular simple ha...
Text Solution
|
- A wave pulse is travelling on a string at 2 m/s. displacement y of the...
Text Solution
|
- Consider the motion of a particle described by x = a cos t , ...
Text Solution
|
- Consider the motion of a particle described by x = a cos t , ...
Text Solution
|
- For a particle moving in the x-y plane, the x and y coordinates are ch...
Text Solution
|