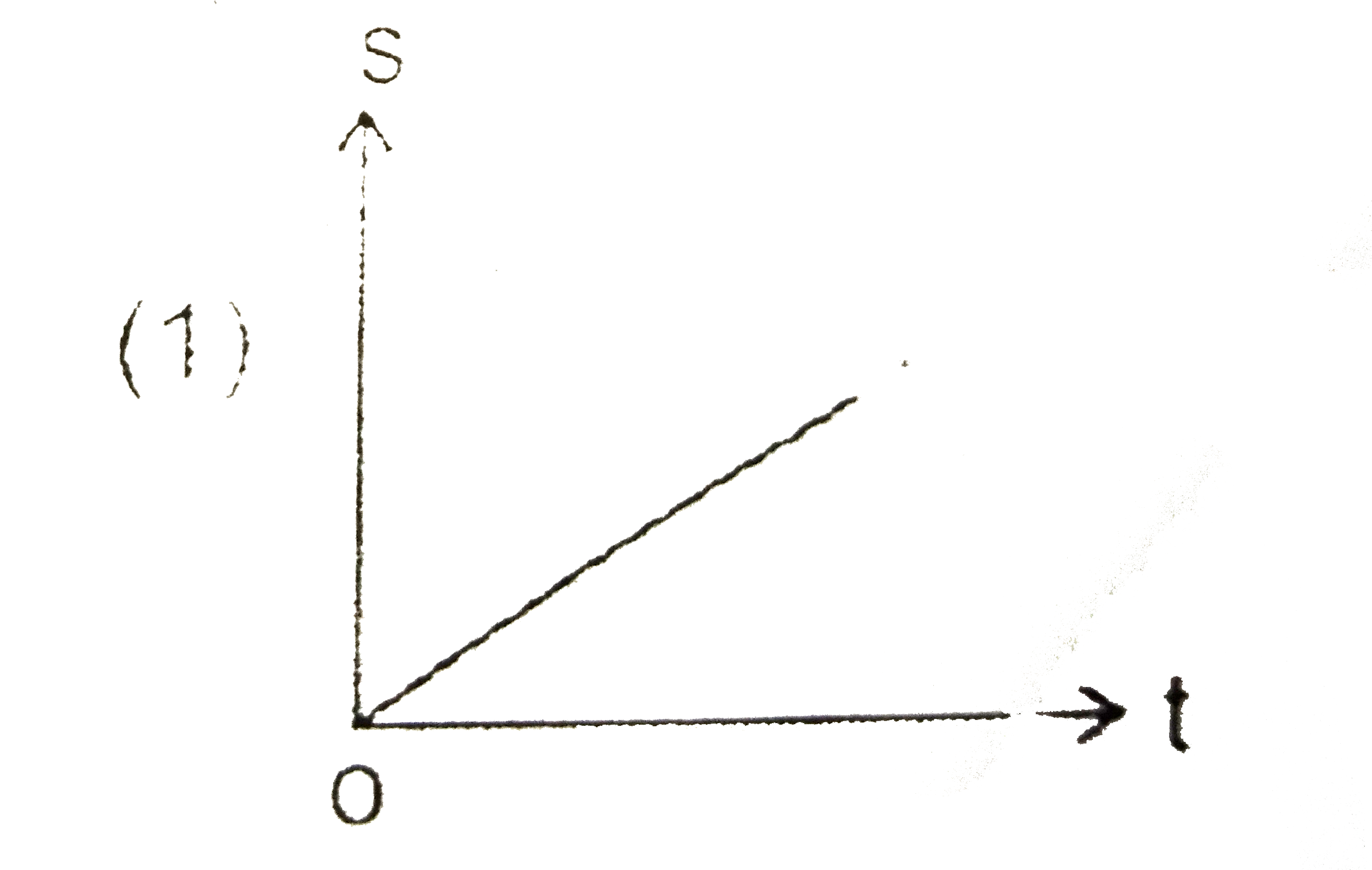
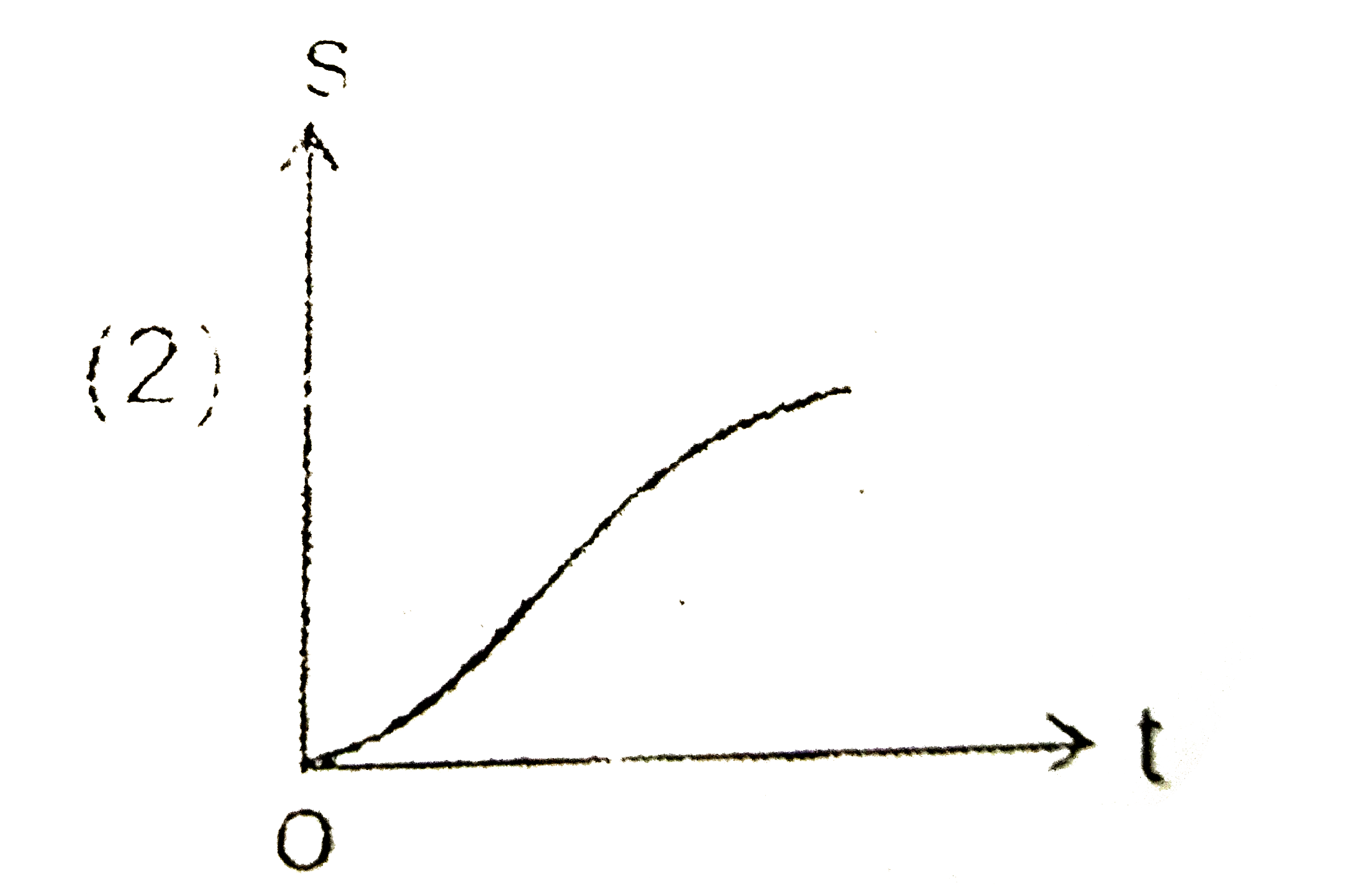
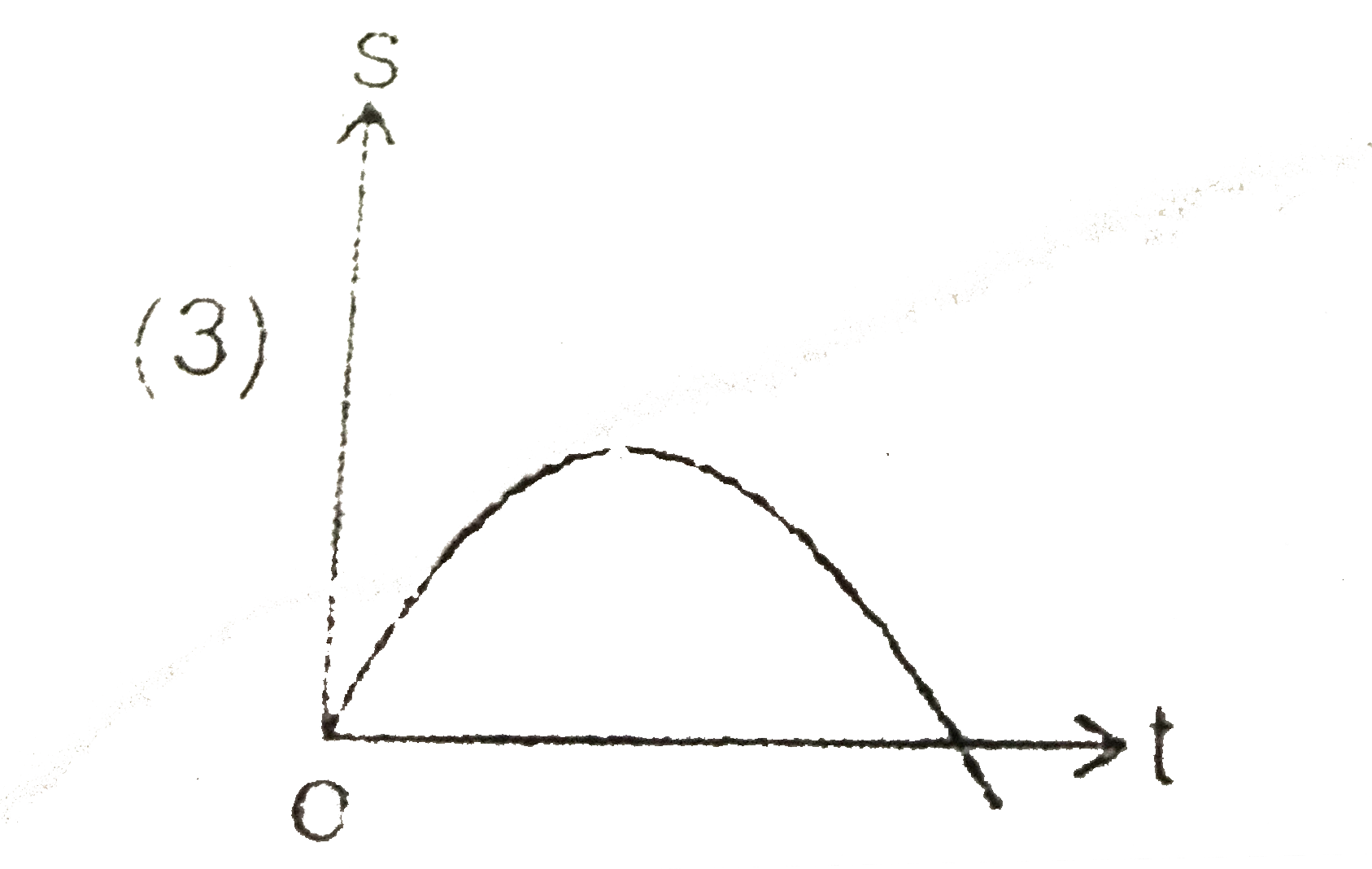
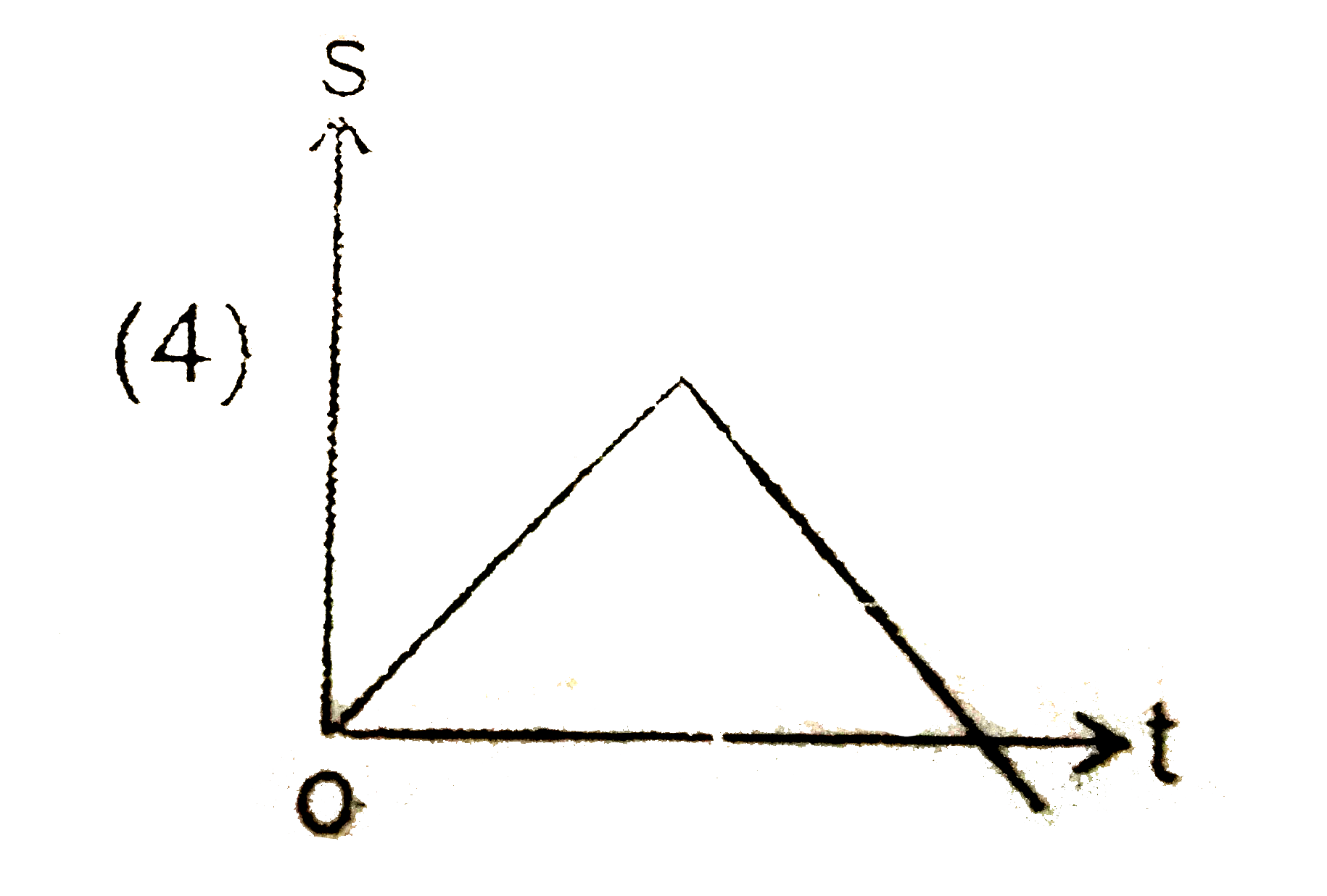
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A particle is moving in x-y plane with y=x/2 and V(x)=4-2t. The displa...
Text Solution
|
- A particle is moving in x-y plane with its x and y co-ordinates varyin...
Text Solution
|
- A particle is moving in x-y plane with y=x/2 and V(x)=4-2t . The displ...
Text Solution
|
- x and y co-ordinates of a particle moving in x-y plane at some instant...
Text Solution
|
- The coordinates of a particle moving in XY-plane very with time as x=4...
Text Solution
|
- A particle moves in the x-y plane. It x and y coordinates vary with ti...
Text Solution
|
- The coordinates of a particle moving in XY-plane vary with time as x= ...
Text Solution
|
- A particle is moving in X-Y plane that x=2t and y=5sin(2t). Then maxim...
Text Solution
|
- Displacement x versus t^(2) graph is shown for a particle. The acceler...
Text Solution
|