Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
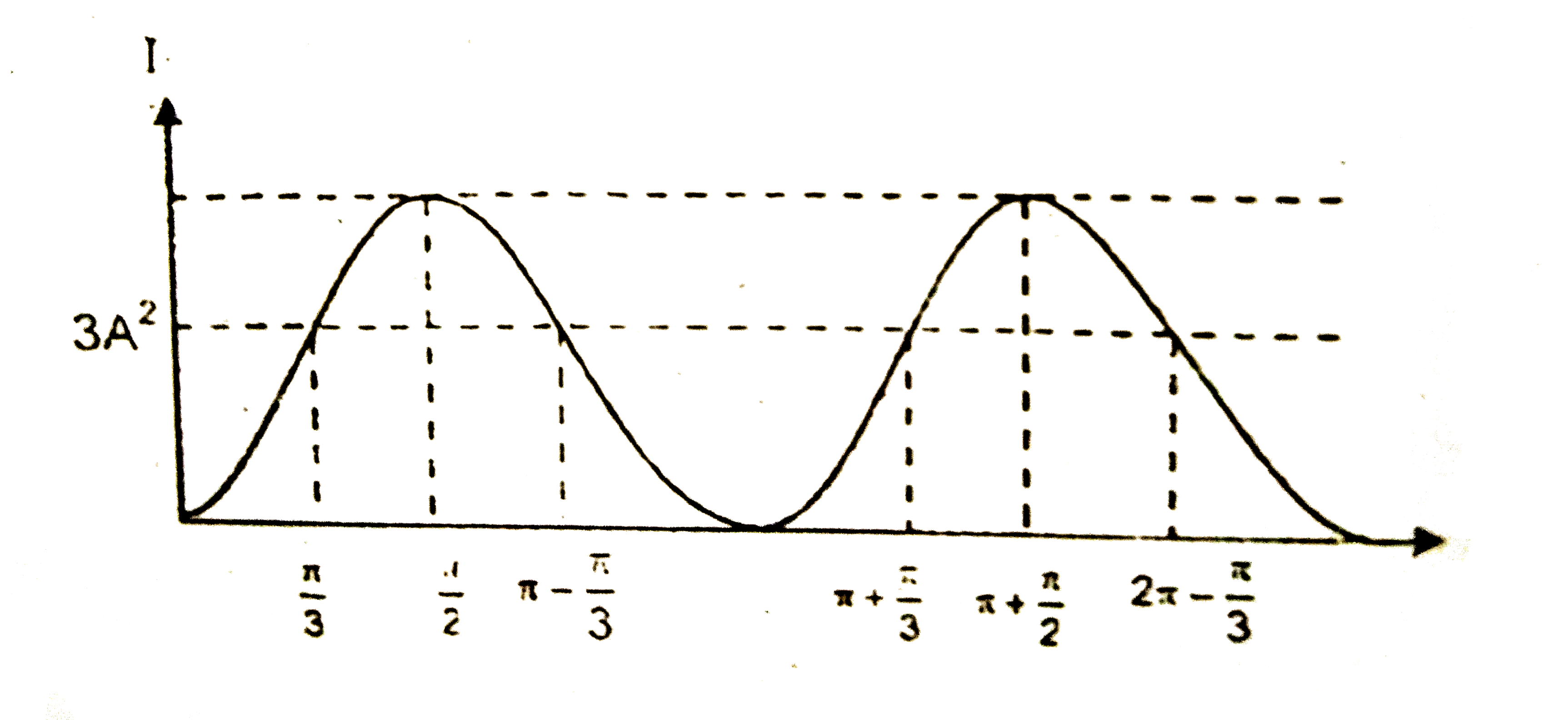
- Two radio signal broadcast their program at the same amplitude A and a...
Text Solution
|
- Two radio stations broadcast their programmes at the same amplitude A ...
Text Solution
|
- Two radio signal broadcast their program at the same amplitude A and a...
Text Solution
|
- Two radio stations broadcast their programmes at the same amplitude A ...
Text Solution
|
- Suppose omega(1) and omega(2) are two distinct cube roots of unity ...
Text Solution
|
- In amplitude modulation, sinusoidal carrier frequency used is denoted ...
Text Solution
|
- Equation of messages signal m = 2 sin omega(m)(t) and carrier signal c...
Text Solution
|
- आयाम मांडुलन में, ज्यावक्रीय वाहक आवृत्ति omega(c) का प्रयोग किया गया ...
Text Solution
|
- दो रेडियो स्टेशन अपने कार्यक्रम समान आयाम A तथा कम अंतर वाली आवृत्तियो...
Text Solution
|