Home
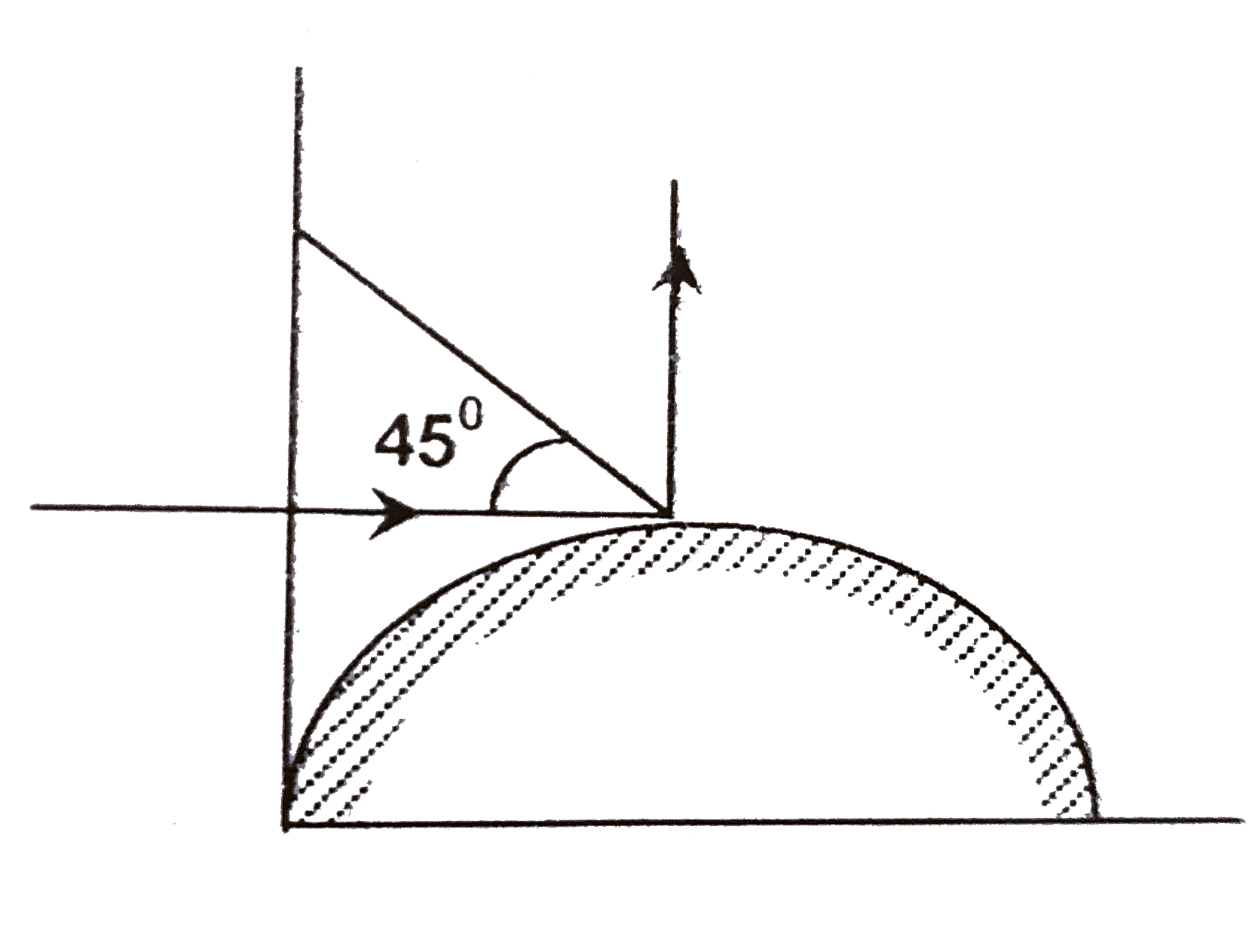
Class 12
PHYSICS
A reflecting surface is represented by t...

A reflecting surface is represented by the equation
`y = (2L)/(pi) sin ((pi x)/(L))`, where `0 le x le L`. A ray of light travelling horizontally becomes vertical after reflection with the surface. The co-ordinates of the point where this ray is incident is.

A

`(L/4,(sqrt(2)L)/(lamda))`

B

`(L/3,(sqrt(3)L)/(pi))`

C

`((3L)/4,(sqrt(2)L)/(lamda))`

D

`((4L)/3,(sqrt(3)L)/(pi))`

Text Solution

Verified by Experts

The correct Answer is:
B
`(dy)/(dx)=2 "cos" ((2x)/L)=-1`
`cos(pix)/L=-1/2`
`x=L/3,(2L)/3`
Promotional Banner

Similar Questions

Explore conceptually related problems

The reflecting surface is represented by the equation 2x =y^2 as shown in the figure. A ray travelling horizontal becomes vertical after reflection. The co-ordinates of the point of incidence are

A refracting surface is represented by the equation x^(2)+y^(2) = a^(2) . A ray travelling in negative x-directed towards positive y-direction after reflection from the surface at point P. Then co-ordinates of point P are

A wave is represented by the equation y= A sin ( 10 pi x + 15 pi l + (pi)/(6)) wher x is in metre and t in second. The expression represents

If the equation of mirror is given by y= 2//pi "sin"pix (y gt 0 , 0 le x le 1 ) then find the point on which horizontal ray should be incident so that the reflected ray become perpendicular to the incident ray

If: sin(x+pi/6)=sqrt3/2 , where 0 le x le 2pi , then: x=

A ray of light coming from origin after reflection at the point P(x,y) of any curve becomes parallel to x-axis,the,equation of the curve may be:

The number of distinct real roots of the equation sqrt(sin x)-(1)/(sqrt(sin x))=cos x("where" 0le x le 2pi) is

The area bounded by the curves y=sin^(-1)|sin x|and y=(sin^(-1)|sin x|)^(2)," where "0 le x le 2pi , is

A ray of light passing through the point (8,3) gets reflected after it meets x -axis at (14,0) .Then the equation of the reflected ray