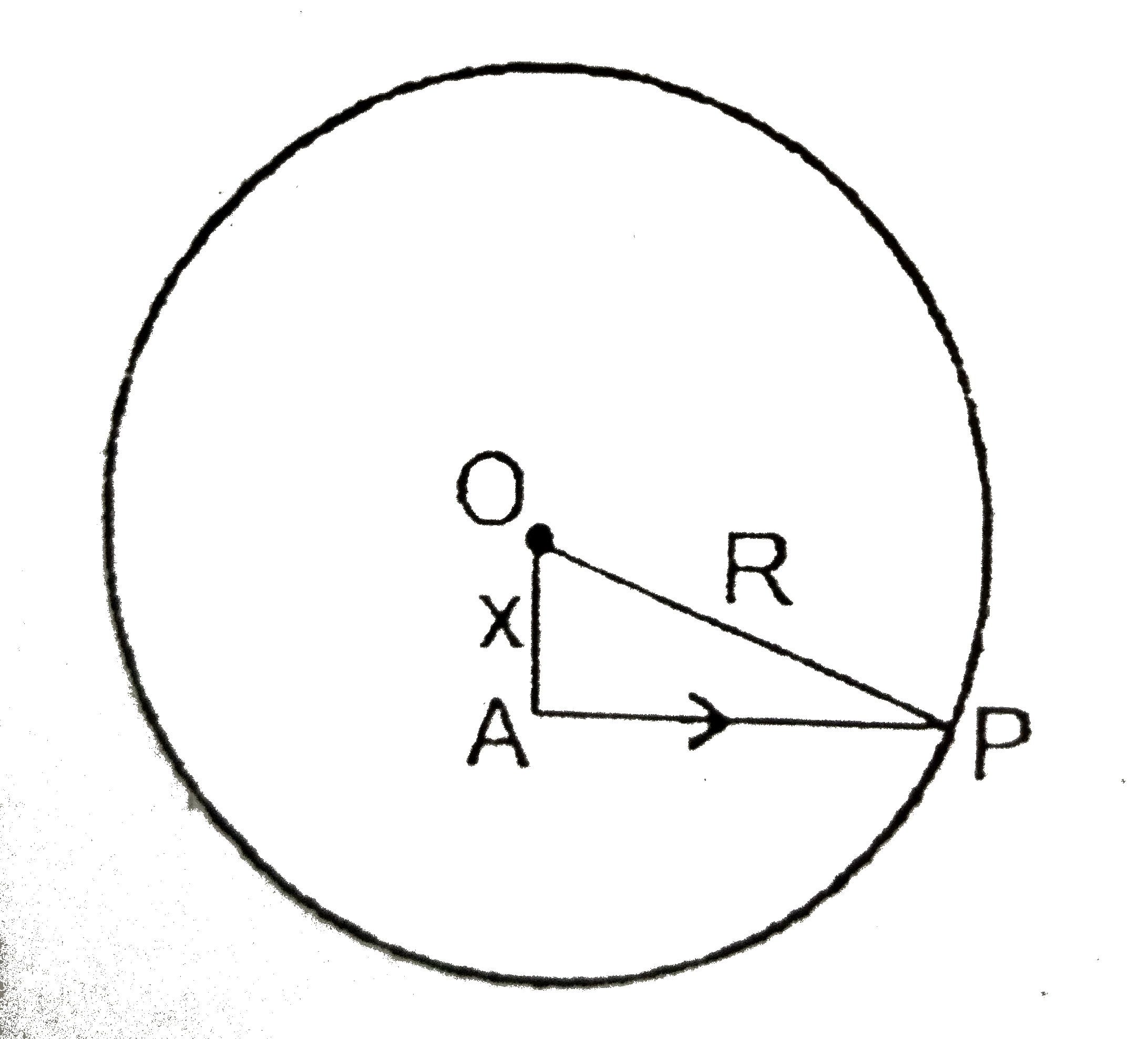
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Inside a solid glass sphere of radius R, a point source of light lies ...
Text Solution
|
- A ray of light is travelling from glass to air. The angle of incidence...
Text Solution
|
- Glass has refractive index mu with respect to air and the critical ang...
Text Solution
|
- A ray of light travelling inside a rectangular glass block of refracti...
Text Solution
|
- Inside a solid glass sphere of radius R, a point source of light lies ...
Text Solution
|
- A ray of light travelling inside a rectangular glass block of refracti...
Text Solution
|
- The Brewster angle for the glass air interface is 54.74^(@) if a ray o...
Text Solution
|
- A light ray is travelling from air to glass. True reflected and refrac...
Text Solution
|
- The Brwster angle of the glass-air interface is 54.74^(@) . If a ray o...
Text Solution
|