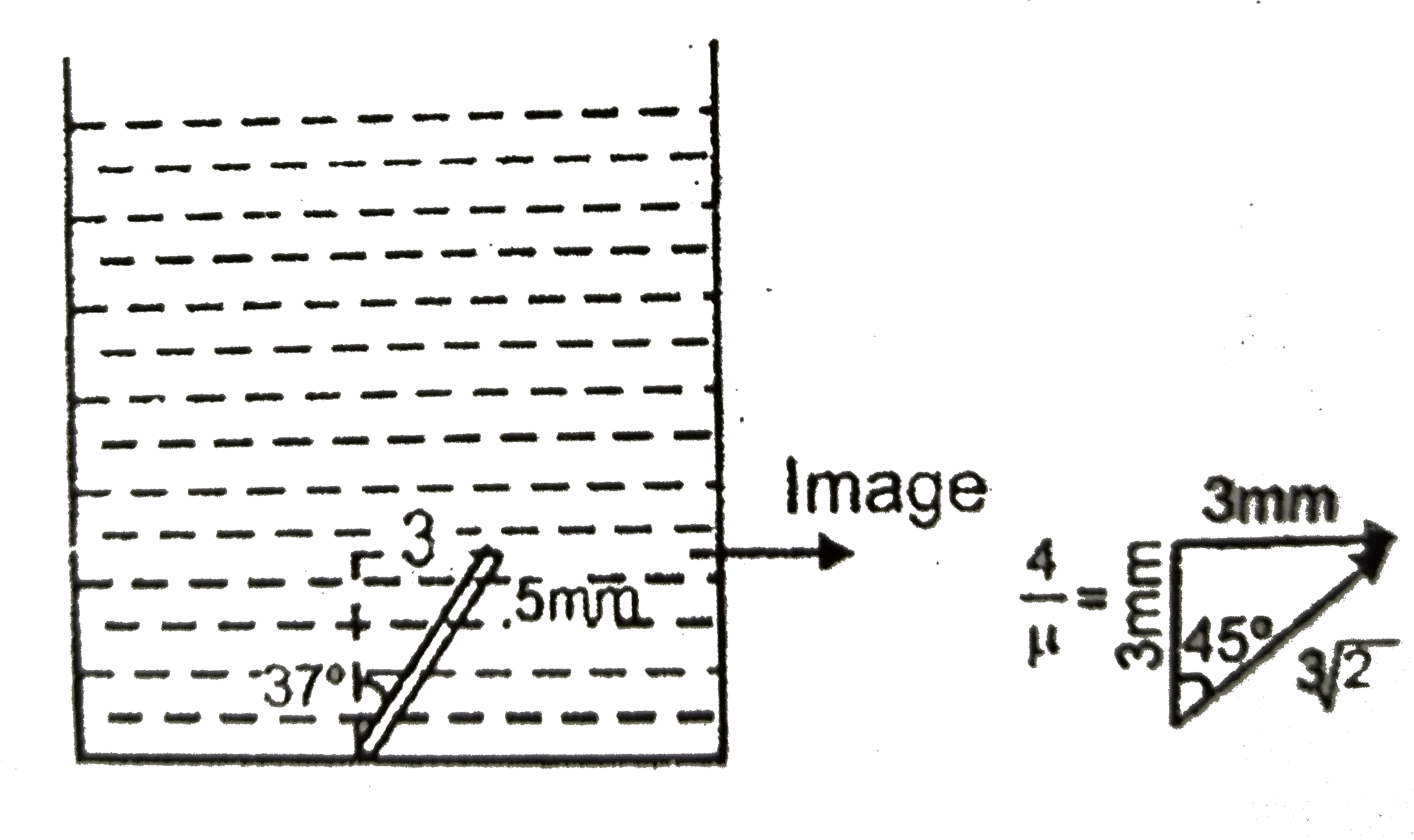Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A small wooden rod of length 5mm is fixed at the bottom of the contain...
Text Solution
|
- A uniform rod pivoted at its upper end hangs vertically. It is displac...
Text Solution
|
- A rod of length l is pivoted about a horizontal , frictionless pin thr...
Text Solution
|
- A wooden rod of a uniform cross section and of length 120 cm is hinged...
Text Solution
|
- A rod of mass m and length l is rotating about a fixed point in the ce...
Text Solution
|
- A small wooden rod of length 5mm is fixed at the bottom of the contain...
Text Solution
|
- A small rod ABC is put in water making an angle 6^(@) with vertical. I...
Text Solution
|
- Two identical small balls are suspended by ends of a rod. Whole assemb...
Text Solution
|
- A rod AB of length L slides in the XY plane. If the rod makes an angle...
Text Solution
|