Text Solution
Verified by Experts
Topper's Solved these Questions
ELECTRIC CURRENT
VGS PUBLICATION-BRILLIANT|Exercise APPLICATION TO DAILY LIFE, CONCERN TO BIODIVERSITY|37 VideosELECTRIC CURRENT
VGS PUBLICATION-BRILLIANT|Exercise FILL IN THE BLANKS|8 VideosELECTRIC CURRENT
VGS PUBLICATION-BRILLIANT|Exercise SECTION - IV (4 Marks Questions)|16 VideosCHEMICAL REACTIONS AND EQUATIONS
VGS PUBLICATION-BRILLIANT|Exercise ESSENTIAL MATERIAL FOR EXAMINATION PURPOSE|1 VideosELECTROMAGNETISM
VGS PUBLICATION-BRILLIANT|Exercise CREATIVE QUESTION FOR NEW MODEL EXAMINATION (SEC-4)|30 Videos
Similar Questions
Explore conceptually related problems
VGS PUBLICATION-BRILLIANT-ELECTRIC CURRENT-CONCEPTUAL UNDERSTANDING
- The second end of a first resistor is connected to first end of second...
Text Solution
|
- Derive an expression for the effective resistance when three resistors...
Text Solution
|
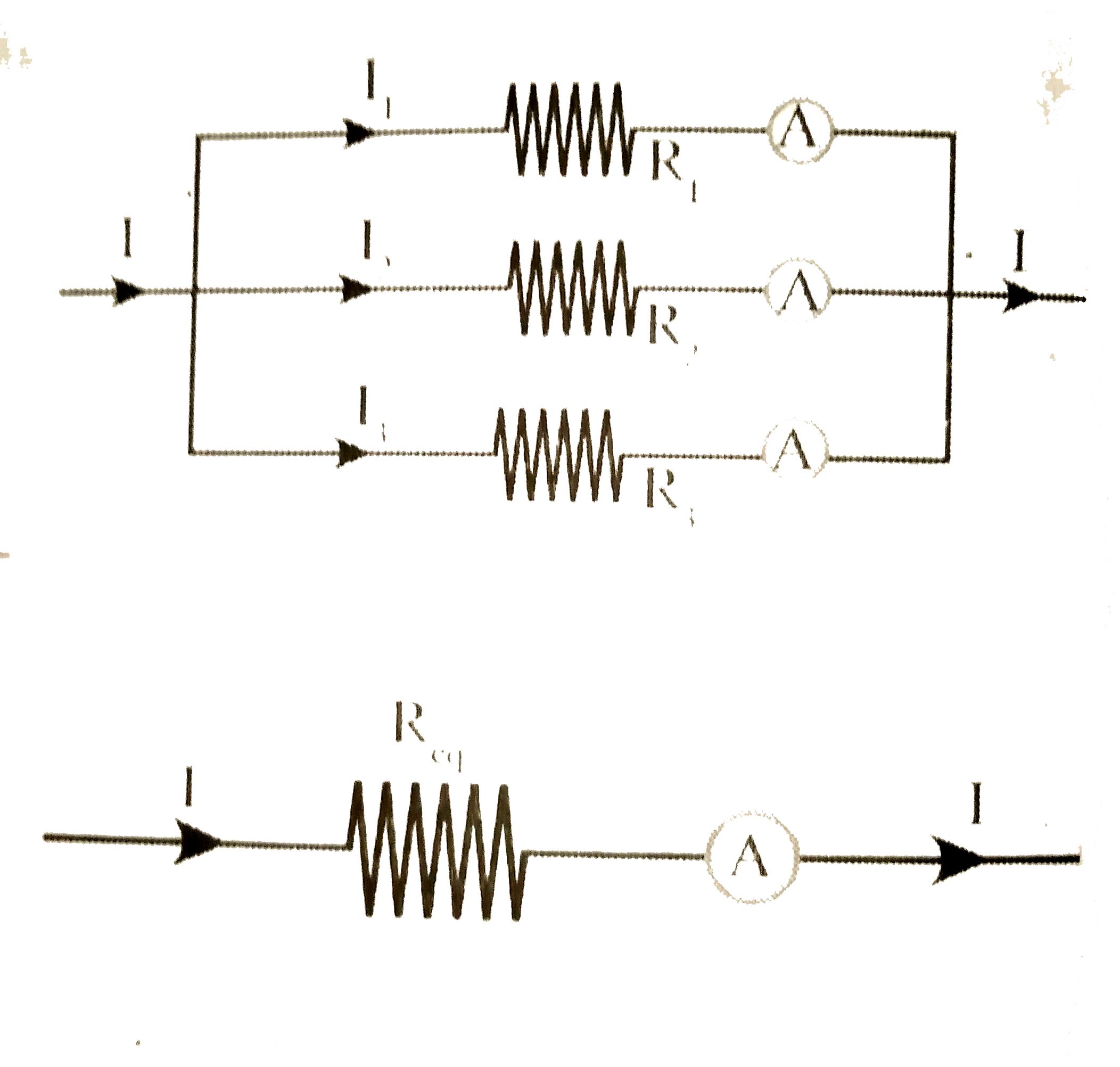
- "Derive"(1)/(Rp)=(1)/(R(1))+(1)/(R(2))+(1)/(R(3)).(Resistors in parall...
Text Solution
|
- Derive an expression for the effective resistance when three resistors...
Text Solution
|
- Derive an expression for the effective resistance when three resistors...
Text Solution
|
- Silver is a better conductor of electricity than copper. Whey do we us...
Text Solution
|
- Two bulbs have ratings 100 W, 220 V and 60 W, 220 V. Which one has the...
Text Solution
|
- Why don't we use series arrangement of electical appliances like bulb,...
Text Solution
|
- A wire of length 1 m and radius 0.1 mn has a resistance of 100Omega. F...
Text Solution
|
- Express the units hom in terms in terms of volt and ampere.
Text Solution
|
- What is a conductor of electricity ?
Text Solution
|
- What is non-conductor ?
Text Solution
|
- Define potential difference and give an expression to it.
Text Solution
|
- State Ohm's law.
Text Solution
|
- What are the limitations of Ohm's law ?
Text Solution
|
- What is resistor ?
Text Solution
|
- Define electric circuit.
Text Solution
|
- State Kirchhoff's Junction Law.
Text Solution
|
- State Kirchhoff's Loop law.
Text Solution
|
- Define electric power.
Text Solution
|