A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
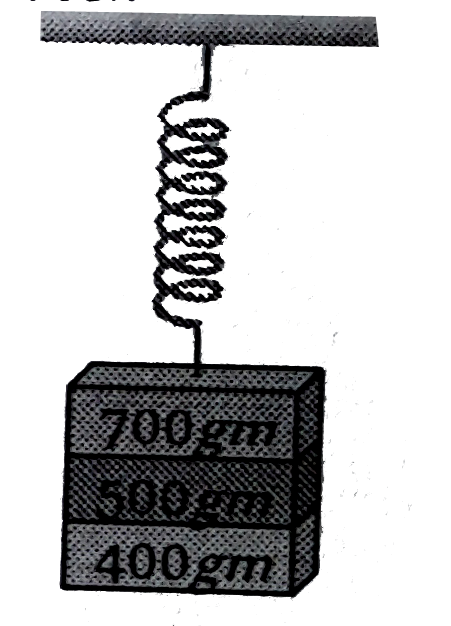
- Three masses 700 g , 500 g , and 400 g are suspended at the end of a s...
Text Solution
|
- Three masses of 500 g , 300 g and 100 g are suspended at the end of a ...
Text Solution
|
- Three masses 700g and 500g and 400g are suspended at the end of a spri...
Text Solution
|
- Three masses 700 g , 500 g , and 400 g are suspended at the end of a s...
Text Solution
|
- Three masses 700g, 500g, and 400 g are suspended at the end of a sprin...
Text Solution
|
- Three mass 0.1 kg ,0.3 kg and 0.4 kg are suspended at end of a spring....
Text Solution
|
- A mass is suspended from a spring have spring constant k is displace...
Text Solution
|
- When a mass of 1 kg is suspended from a spring, it is stretched by 0.4...
Text Solution
|
- Three masses 0.1 kg, 0.3 and 0.4 kg are suspended at the end of the sp...
Text Solution
|