Home
Class 11
PHYSICS
A body performs S.H.M. Its kinetic energ...

A body performs S.H.M. Its kinetic energy K varies with time t as indicated by graph

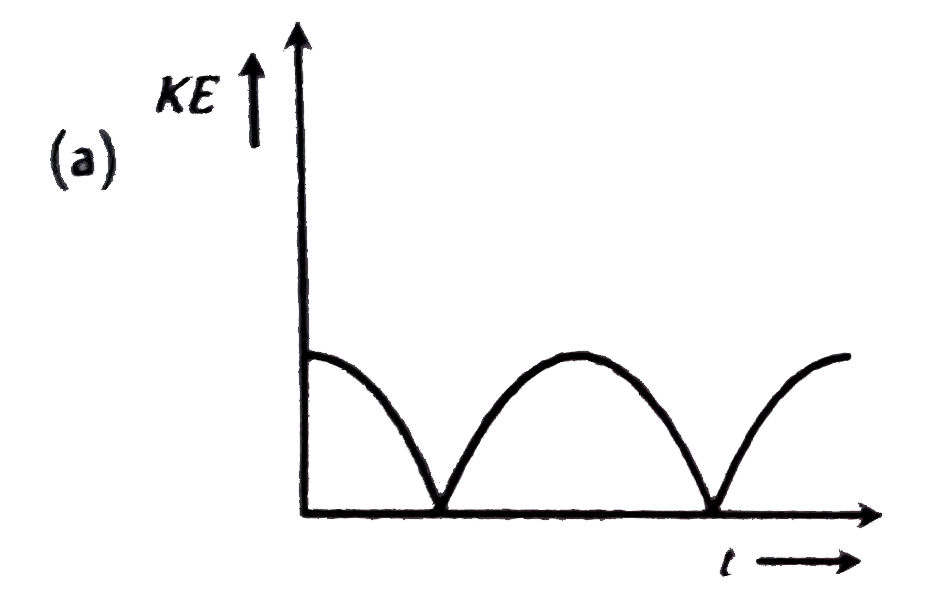
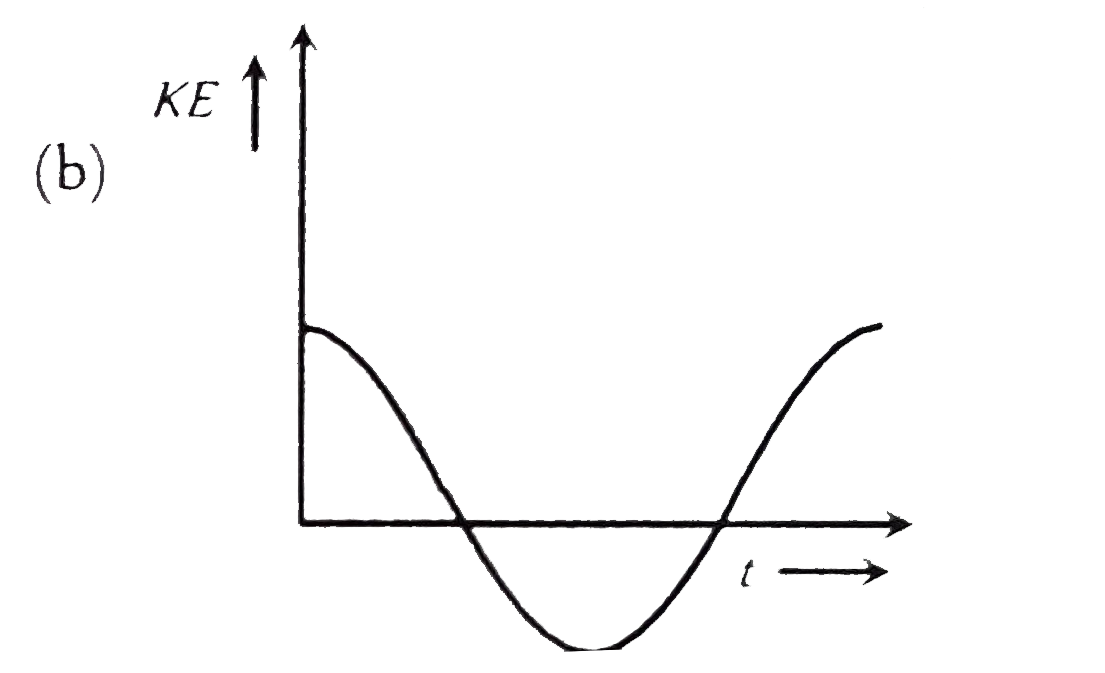
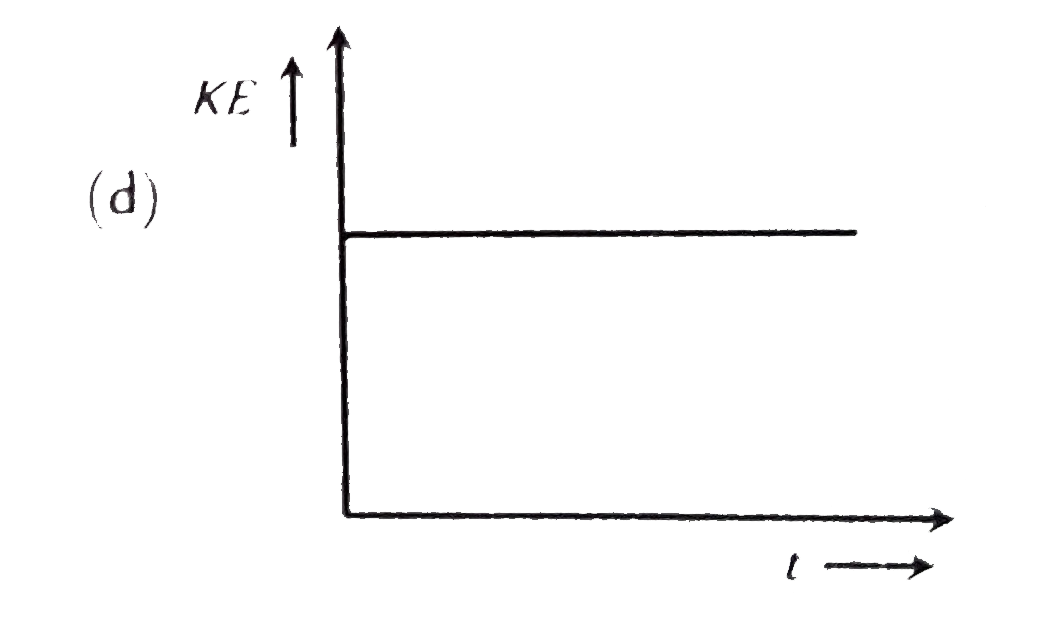
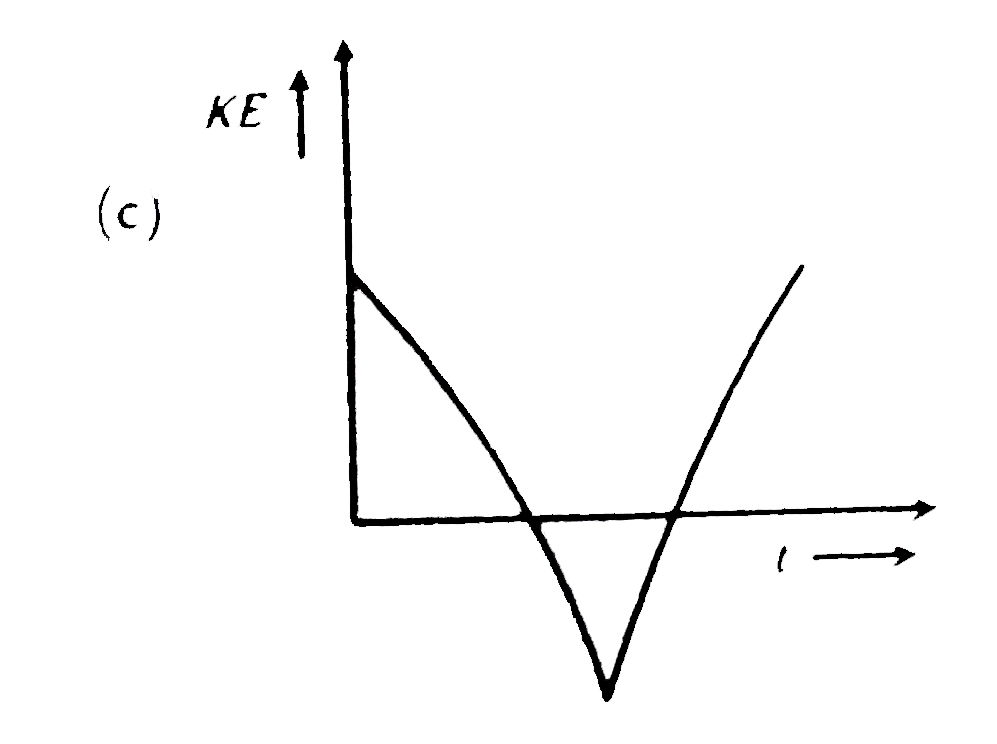A

B

C

D

Text Solution

Verified by Experts

The correct Answer is:
A
Promotional Banner

Topper's Solved these Questions

  • SIMPLE HARMONIC MOTION

    ERRORLESS |Exercise Assertion & Reason|23 Videos

  • SIMPLE HARMONIC MOTION

    ERRORLESS |Exercise simple Harmonic Motion|21 Videos

  • SIMPLE HARMONIC MOTION

    ERRORLESS |Exercise Superposition of S.H. M and Resonance|14 Videos

  • ROTATIONAL MOTION

    ERRORLESS |Exercise Practice Problems (Problems based on motion of connected mass)|10 Videos

  • SURFACE TENSION

    ERRORLESS |Exercise Exercise|214 Videos

Similar Questions

Explore conceptually related problems

As a body performs SHM its potential energy U. varies with time as indicated in

A particle is performing SHM. Its kinetic energy K varies with time t as shown in the figure. Then

A body is performing SHM, then its

A body is performing SHM , then its

When a particle performs S.H.M., its kinetic energy varies periodically. If the frequency of the particle is 10, then the kinetic energy of the particle will vary with frequency equal to

A particle starts moving from the origin & moves along positive x-direction. Its rate of change of kinetic energy with time shown on y-axis varies with time t as shown in the graph. If position, velocity acceleration & kinetic energy of the particle at any time t are x,v a & k respectively then which of the option (s) may be correct ?

In S.H.M., the graph between kinetic energy K and time 't' is

A body of mass 1 kg starts moving from rest t = 0 in a circular path of radius 8 m. Its kinetic energy varies with time as k = 2t^(2) J then magnitude of centripetal acceleration ( in m//s^(2) ) at t = 2s is.

A body of mass 4kg moving along a straight line under the action of a force.If kinetic energy varies with time as k=8t .The force acting on the body is ?

A body performs SHM along the straight line MNOPQ. Its kinetic energy at N and at P is half of its peak value of O. If the time period is T, then the time taken to travel from N to P directly along MOP is