माना m द्रव्यमान का साइकिल सवार v वेग से। त्रिज्या के वृत्तीय मार्ग पर चल रहा है । इस समय साइकिल पर निम्नलिखित चार बल कार्य करेंगे -
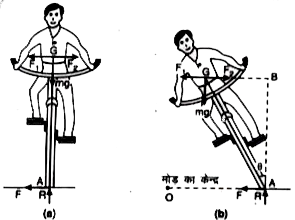
(i) अभिकेन्द्रीय बल `(mv^2)/(r)` बिन्दु A पर मोड़ के केन्द्र की ओर। (ii) सड़क तथा साइकिल के पहियों के बीच घर्षण बल F मार्ग के केन्द्र की ओर। (iii) साइकिल तथा सवार का कुल भार mg ऊर्ध्वाधरतः नीचे की ओर । (iv) पृथ्वी की आभलम्ब प्रतिक्रिया R(=mg) ऊर्ध्वाधरतः ऊपर की ओर।
यदि साइकिल सवार मोड़ पर सीधा रहता है [चित्र (a)] तो भार mg तथा प्रतिक्रिया R परस्पर विपरीत दिशा में होने के कारण एक-दूसरे को निष्फल कर देते हैं तथा बल `F_1 " व " F_2 (= F)` दक्षिणावर्ती बलयुग्म बनाते हैं जिससे सवार बाहर की ओर गिरने लगता है।
यदि सवार मोड़ के केन्द्र की ओर ऊर्ध्वाधर से `theta` कोण बनाता हुआ झुक जाता है [(b)], तो उसका भार mg तथा प्रतिक्रिया बल R(=mg) एक वामावर्ती बलयुग्म बनाते हैं जो `F_1` तथा `F_2 (=F)` द्वारा बने दक्षिणावर्ती बलयुग्म को सन्तुलित कर देता है। अतः सन्तुलन की स्थिति में,
वामावर्त बलयुग्म का आघूर्ण = दक्षिणावर्त बलयुग्म का आघूर्णी
`mg xx GB = Fxx AB`
चित्र (b) से, समकोण त्रिभुज ABG में, AB = GA `cos theta`
तथा `GB = GA sin theta`
`therefore mg xx GA sin theta = F xx GA cos theta`
`(sin theta)/(cos theta) = (F)/(mg) " " [ because F = (mv^2)/(r) ]`
`tan theta = (mv^2 //r)/(mg) = (v^2)/(rg)`
` tan theta = (v^2)/(rg)`
` tan theta = tan^(-1) (v^2)/(rg)`
साइकिल सवार का सन्तुलन बनाए रखने के लिए `theta` का मान न्यूनतम होना चाहिए। `theta` के न्यूनतम मान के लिए। का मान कम तथा का मान अधिक होना चाहिए। इसी कारण साइकिल सवार मोड़ने की दिशा में झुककर अपना वेग कम करके अधिक त्रिज्या का पथ अपनाता है
