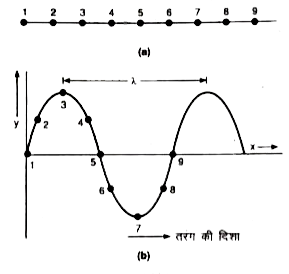
समीकरण की स्थापना-माना किसी माध्यम में प्रगामी तरंग धनात्मक X-अक्ष की ओर संचरित हो रही है.[चित्र (a)] । इसमें माध्यम के कणों 1,2, 3...की साम्य स्थितियाँ प्रदर्शित हैं। तरंग के संचरित होने पर माध्यम के कण अपनी साम्य स्थिति के दोनों तरफ कम्पन करते हैं। किसी क्षण t पर कणों की स्थितियाँ चित्र (b) में प्रदर्शित हैं। कणों की इन स्थितियों को मिलाने पर प्राप्त वक्र ही प्रगामी तरंग प्रदर्शित करता है।
माना, मूल बिन्दु O पर स्थित कण 1 प्रारम्भ में (t=0) पर अपना कम्पन्न प्रारम्भ करता है। यदि t सेकण्ड पश्चात् इस कण का विस्थापन y हो, तो
` y = a sin omega t " " ....(1)`
तथा ` omega = 2pi n = 2pi //T`
जैसे-जैसे तरंग, कण 1 से आगे बढ़ती जाती है, अन्य कण भी अपना कम्पन करना प्रारम्भ कर देते हैं। यदि तरंग की चाल v है, तो कण '1' से x दूरी पर स्थित कण '6' तक तरंग को पहुँचने में x/v सेकण्ड समय लगेगा। अतः मूल बिन्दु से दूरी पर स्थित कण '6', कण '1' से x/v सेकण्ड पश्चात् कम्पन प्रारम्भ करेगा। स्पष्टतः किसी क्षण । पर कण '6' का विस्थापन वही होगा जो उस क्षण से x/v सेकण्ड पहले [अर्थात् (t - x/v)] कण '1' का था। अत: मूल बिन्दु से - दूरी पर स्थित कण '6' का t समय पर विस्थापन
` y = a sin omega (t - v/x) =a sin (2pi)/(T) ( t- x/v)`
` y =a sin (2pi)/(vT) (vt - x) a sin (2pi)/(lamda) (vt- x)`
अतः धनात्मक X - अक्ष की दिशा में संचरित प्रगामी तरंग का समीकरण
` y = a sin omega ( t - x/v) =a sin (2pi)/(lamda) (vt - x) =a sin 2pi ( t/T - x/lamda)`
