Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
ANURAG MISHRA-DESCRIPTION OF MOTION-Level-3
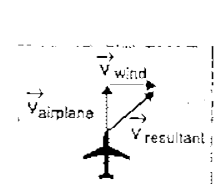
- Similarly if an airplane moves in a wind its resultant velocity will b...
Text Solution
|
- A particle 'A' starts moving frorri point A with constant velocity 4 m...
Text Solution
|
- A particle 'A' starts moving frorri point A with constant velocity 4 m...
Text Solution
|
- A particle 'A' starts moving frorri point A with constant velocity 4 m...
Text Solution
|
- A particle 'A' starts moving frorri point A with constant velocity 4 m...
Text Solution
|
- A particle 'A' starts moving frorri point A with constant velocity 4 m...
Text Solution
|
- A particle 'A' starts moving frorri point A with constant velocity 4 m...
Text Solution
|
- A particle 'A' starts moving frorri point A with constant velocity 4 m...
Text Solution
|
- A swimmer wishes to .cross a river 500 m wide flowing at a rate 'u'. H...
Text Solution
|
- A swimmer wishes to cross a river 500 m wide flowing at a rate 'u'. Hi...
Text Solution
|
- A swimmer wishes to cross a river 500 m wide flowing at a rate 'u'. Hi...
Text Solution
|
- A swimmer wishes to cross a river 500 m wide flowing at a rate 'u'. Hi...
Text Solution
|
- A swimmer wishes to cross a river 500 m wide flowing at a rate 'u'. Hi...
Text Solution
|
- A swimmer wishes to cross a river 500 m wide flowing at a rate 'u'. Hi...
Text Solution
|
- A swimmer wishes to cross a river 500 m wide flowing at a rate 'u'. Hi...
Text Solution
|
- A particle is fired from A in the diagonal plane of a building of dime...
Text Solution
|
- A particle is fired from 'A' in the diagonal plane of building of dime...
Text Solution
|
- A particle is fired from A in the diagonal plane of a building of dime...
Text Solution
|
- A particle is fired from A in the diagonal plane of a building of dime...
Text Solution
|
- A particle is fired from A in the diagonal plane of a building of dime...
Text Solution
|
- A dart gun is fired towards a Squirrel hanging from a tree. Dart gun w...
Text Solution
|