Home
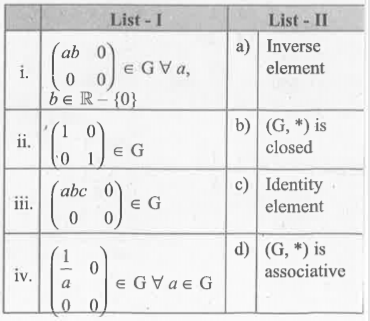
Class 12
MATHS
Let G{({:(a,0),(0,0):})}//a in R-{0}} an...

Let `G{({:(a,0),(0,0):})}//a in R-{0}}` and `**` is the matrix multiplication.

The Correct match is

A

(i)-b, (ii)-c, (iii)-d, (iv)-a

B

(i)-a, (ii)-b, (iii)-c, (iv)-d

C

(i)-b, (ii)-c, (iii)-d, (iv)-a

D

(i)-d, (ii)-c, (iii)-b, (iv)-a

Text Solution

Verified by Experts

The correct Answer is:
A
Promotional Banner

Topper's Solved these Questions

  • DISCRETE MATHEMATICS

    SURA PUBLICATION|Exercise 2 MARKS|6 Videos

  • DISCRETE MATHEMATICS

    SURA PUBLICATION|Exercise 3 MARKS|5 Videos

  • DISCRETE MATHEMATICS

    SURA PUBLICATION|Exercise CHOOSE THE INCORRECT STATEMENT:|5 Videos

  • DIFFERENTIALS AND PARTIAL DERIVATIVES

    SURA PUBLICATION|Exercise 5 MARKS|4 Videos

  • INVERSE TRIGONOMETRIC FUNCTIONS

    SURA PUBLICATION|Exercise ADDITIONAL QUESTIONS ( 5 MARKS)|6 Videos

Similar Questions

Explore conceptually related problems

(i) Let M={({:(x,x),(x,x):}):x in R -{0}} and let ** be the matrix multiplication. Determine whether M is closed under ** . If so, examinie the existence of identity, existence of inverse properties for the operation ** on M.

Let M={[{:(,x,x),(,x,x):}}: x in R-{0}} and let * be the matrix multiplication. Determine whether M is closed under *. If so, examine the commutative and associative properties satisfied by * on M.

Let M={[{:(,x,x),(,x,x):}}: x in R-{0}} and let * be the matrix multiplication. Determine whether M is closed under *. If so, examine the existence of identify, existence of inverse properties for the operation * on M.

The identify element of {({:(x,x),(x,x):})} x in R, x ne 0} under matrix multiplication is

Let P=(-1, 0), Q=(0,0) and R=(3, 3sqrt3 ) be three points. The equation of the bisector of the angle PQR is

Let a and b be two real numbers such that a > 1, b > 1. If A=[(a,0), (0,b)] , then lim_(n to oo) A^(-n) is a. unit matrix b. null matrix c. 2l d. none of these

Match list {:(" ", "List I"," " ,"List II"), (i., [{:(a, b), (b, a):}], (a), "identity"), (ii., [{:(0, b), (-b, 0):}], (b), "Singular matrix"), (iii., [{:(a, a), (b, b):}], (c), "Skew-Symmetric"), (iv., [{:(1,0), (0,1):}], (d), "Symmetric"):} The correct match is (i) (ii) (iii) (iv)

Let A={0, 1} and B={0, 1} then AtimesB =