Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
ANURAG MISHRA-WORK AND ENERGY-Eample
- A uniform chain of mass m and length llt(piR)/(2) is placed on a smoot...
Text Solution
|
- A pendulum bob is suspended on a flat car that moves with velocity v(0...
Text Solution
|
- A pendulum bob can swing along a ciircular path on a smooth inclined p...
Text Solution
|
- A small toy car of mass m slides with negligible friction on a ''loop'...
Text Solution
|
- A small ball is rolled with speed u from point A along a smooth circul...
Text Solution
|
- A block of mass m is pressed against a spring of force constant k. The...
Text Solution
|
- A particle attached to a vertical string of length 1m is projected hor...
Text Solution
|
- A particle is suspended by a light vertical inelastic string of length...
Text Solution
|
- A small ball is hung as shown an a string of length L. (a) If v(0) g...
Text Solution
|
- A simple pendulum swings with angular amplitude theta. The tension in ...
Text Solution
|
- A heavy particle hanging from a string of length l is projected horizo...
Text Solution
|
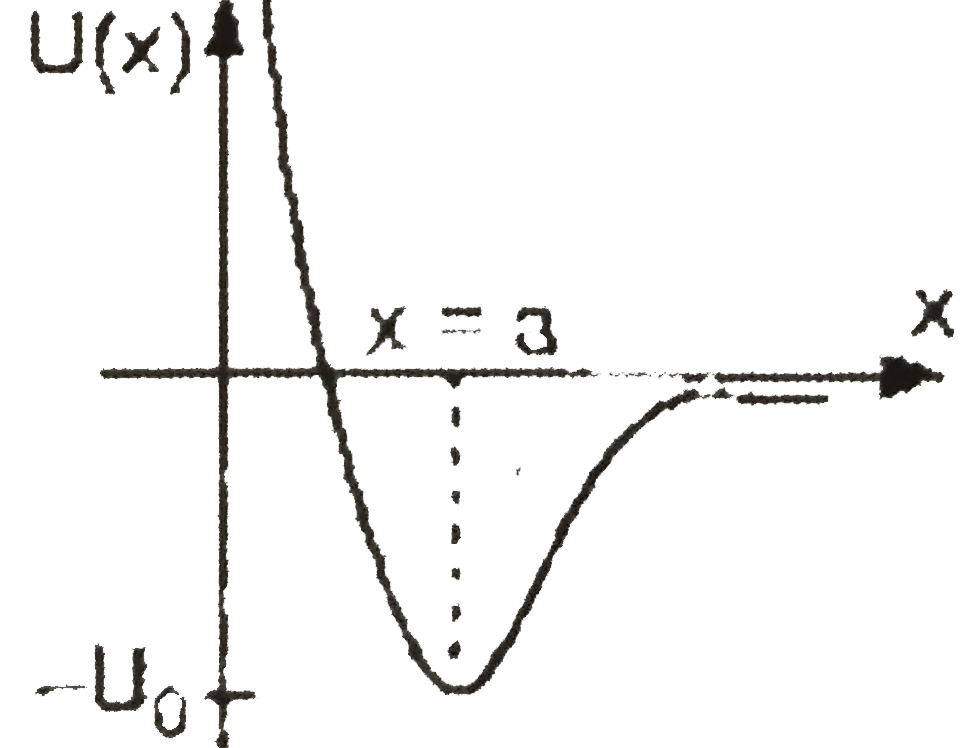
- The force between two atoms in a diatomic molecule can be represented ...
Text Solution
|
- A body of mass 2 kg is moving under the influence of a central force w...
Text Solution
|
- A single conservative force F(x) acts on a 1.0-kg particle that moves ...
Text Solution
|
- Consider a one-dimensional motion of a particle with total energy E. T...
Text Solution
|
- Two particle of mass m and 2m, connected by a massless rod, slide on t...
Text Solution
|
- The figure shows a pendulum of length l suspended at a distance x vert...
Text Solution
|
- Two blocks are connected by a massless string that passes over a frict...
Text Solution
|
- Fig. 3E.47 (a) shows a circular ring of mass M that hangs in a vertica...
Text Solution
|
- A force acting on a certain particle depends of the particles position...
Text Solution
|