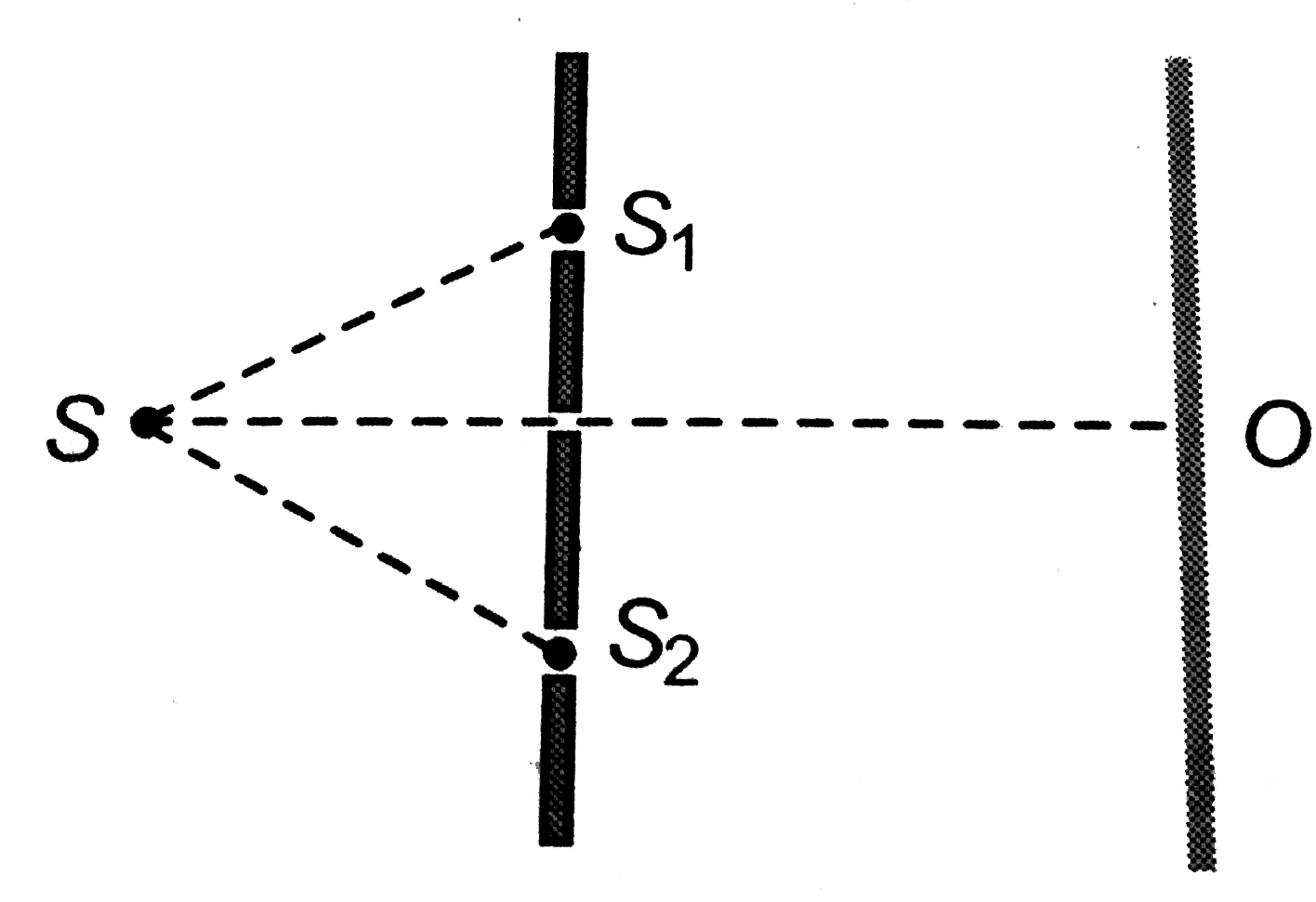
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- In the set up shown in figure, the two slits S1 and S2 are not equidis...
Text Solution
|
- In a Young's double slit set up, the wavelength of light used is 54nm....
Text Solution
|
- In a Young's double slits set up, the wavelength of light used is 546n...
Text Solution
|
- A parallel beam of light (lambda= 5000 Å) is incident at an angle thet...
Text Solution
|
- In the set up shown in figure, the two slits S1 and S2 are not equidis...
Text Solution
|
- In an interference experiment, the two slits S(1) and S(2) are not equ...
Text Solution
|
- चित्र में दिखाई गई व्यवस्था में S1 व S2 स्लिट S से बराबर दूरियों पर नह...
Text Solution
|
- यंग के द्विस्लिट प्रयोग में, माना S1 व S2 दो स्लिटें हैं तथा C परदे का...
Text Solution
|
- Light of wavelength lambda= 500 nm falls on two narrow slits placed a ...
Text Solution
|