Topper's Solved these Questions
LINEAR MOMENTUM & ITS CONSERVATION
PHYSICS GALAXY - ASHISH ARORA|Exercise Practive Exercise|28 VideosLINEAR MOMENTUM & ITS CONSERVATION
PHYSICS GALAXY - ASHISH ARORA|Exercise Discussio Q|28 VideosKINEMATICS
PHYSICS GALAXY - ASHISH ARORA|Exercise Unsolved Numerical Pro.|83 VideosNEWTONS LAWS OF MOTION
PHYSICS GALAXY - ASHISH ARORA|Exercise Unsolved Numerical Problem|81 Videos
Similar Questions
Explore conceptually related problems
PHYSICS GALAXY - ASHISH ARORA-LINEAR MOMENTUM & ITS CONSERVATION-exercise 1.3
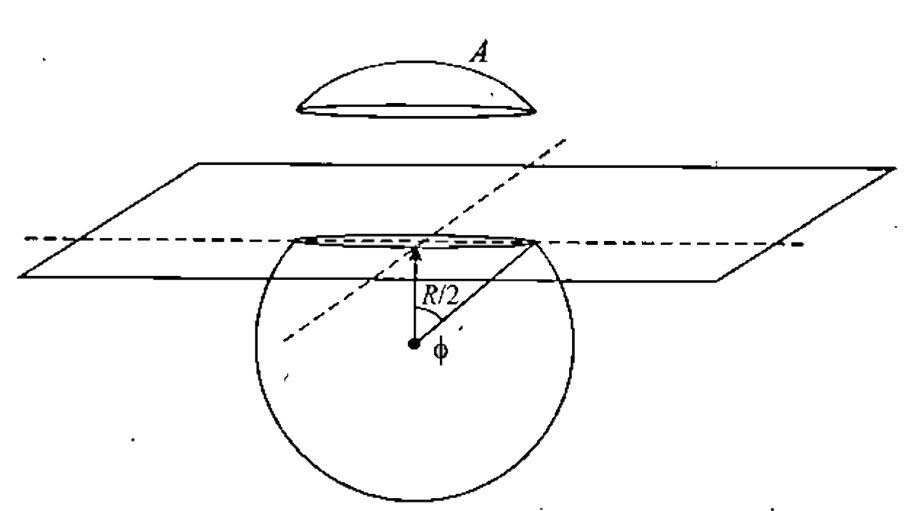
- From a solid sphere a small part A is cut by a plane at a distance R//...
Text Solution
|
- An isolated particle of mass m is moving in horizontal plane xy along ...
Text Solution
|
- A shell at rest at origin explodes into three fragments of masses 1 kg...
Text Solution
|
- A small block of mass m starts sliding down from rest along the smooth...
Text Solution
|