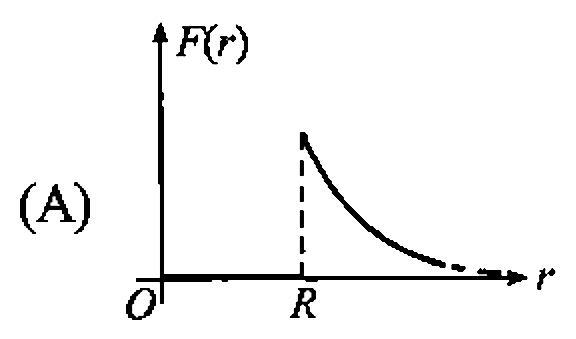
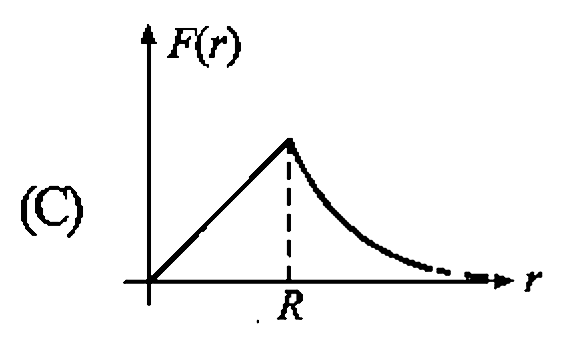
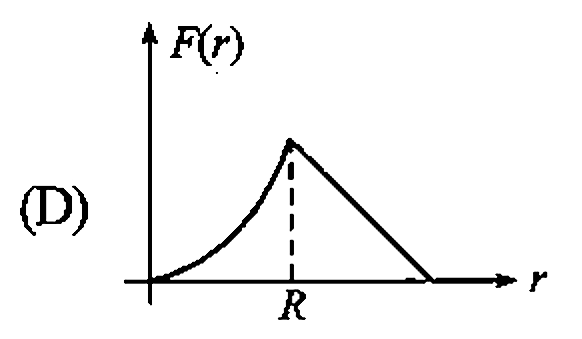
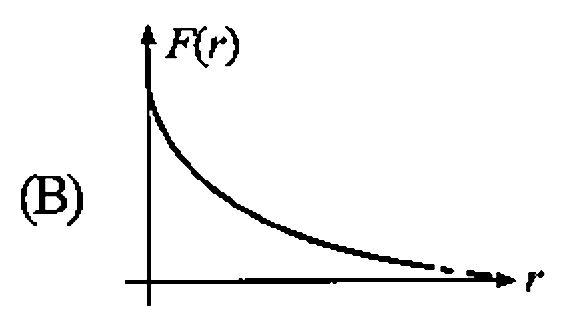A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
GRAVITATION
PHYSICS GALAXY - ASHISH ARORA|Exercise Numerial MCQs|59 VideosGRAVITATION
PHYSICS GALAXY - ASHISH ARORA|Exercise Advance MCQs|17 VideosGRAVITATION
PHYSICS GALAXY - ASHISH ARORA|Exercise Discussion Qns|31 VideosFLUID MECHANICS
PHYSICS GALAXY - ASHISH ARORA|Exercise Unsolved Numerical Problems|86 VideosKINEMATICS
PHYSICS GALAXY - ASHISH ARORA|Exercise Unsolved Numerical Pro.|83 Videos
Similar Questions
Explore conceptually related problems
PHYSICS GALAXY - ASHISH ARORA-GRAVITATION-Concetual MCQ
- A particle is placed in a field characterized by a value of gravitatio...
Text Solution
|
- Which of the following statement is wrong ?
Text Solution
|
- If the period of revolution of an artificial satellite just above the ...
Text Solution
|
- A planet is revolving round the sun in an elliptical orbit. Of the fol...
Text Solution
|
- Two air bubble in water ina continer in gravity free space:
Text Solution
|
- A particle of mass m is ocated at a distance r from the centre of she...
Text Solution
|
- A sphare of mass M and radiusR(2) has a concentric cavity of radius ...
Text Solution
|
- A shell of mass M and radius R has point mass m placed at a distance r...
Text Solution
|
- A satellite is orbiting round the earth. While in orbit a small part s...
Text Solution
|
- A satellite S is moving in an elliptical orbit around the earth. The m...
Text Solution
|
- A planet of mass m is moving around the sun in an elliptical orbit of ...
Text Solution
|
- Two stars of masses m(1) and m(2) distance r apart, revolve about thei...
Text Solution
|
- A satellite in an equatorial orbit has a time period of 6 hrs, At a ce...
Text Solution
|
- A planet moves around the sun. at a given point P, it is closest fro...
Text Solution
|
- A tunnel is made inside earth passing throgh centre of earth. A partic...
Text Solution
|
- Two particle A and B (of masses m and 4m) are released from rest in th...
Text Solution
|
- Identify the correct defination of gravitationa potential at a point.
Text Solution
|
- Tidal waves in the sea are primarily due to
Text Solution
|
- If the sun were suddenly replaced by a block hole of one solar mass, w...
Text Solution
|
- A block of mass m is lying at a distance r from a spherical shell of m...
Text Solution
|