Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
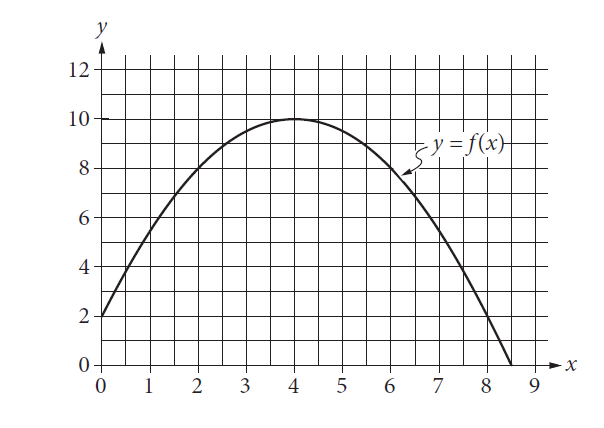
- The graph of the function f, defined by f(x)=-1/2(x-4)^2 +10, is shown...
Text Solution
|
- Match the following Column A to Column B
Text Solution
|
- The inequation represented by the graph given below is : <img src="htt...
Text Solution
|
- The inequation that best describes the graph given below is <img src=...
Text Solution
|
- The inequation that best describes the following graph is <img src="h...
Text Solution
|
- In Fig, find the value of x. ltimg src="https://d10lpgp6xz60nq.cloud...
Text Solution
|
- At x=0, value of (dy)/(dx) is : ltimg src="https://d10lpgp6xz60nq.clou...
Text Solution
|
- Graph of an exponential function y=2+ae^(-x) is shown in figure. What ...
Text Solution
|
- What is the distance OA for the square shown in figure :- ltimg src="h...
Text Solution
|