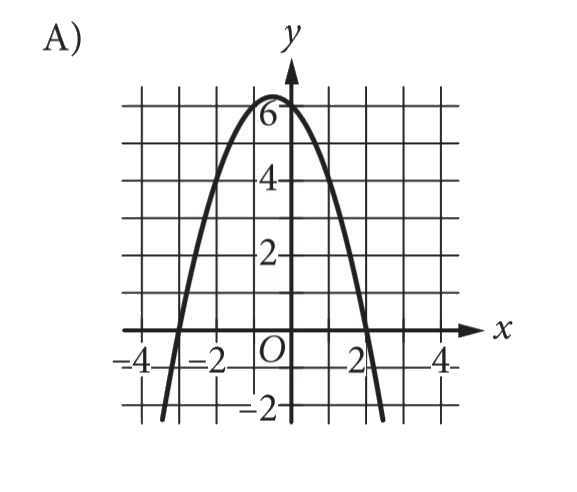
A
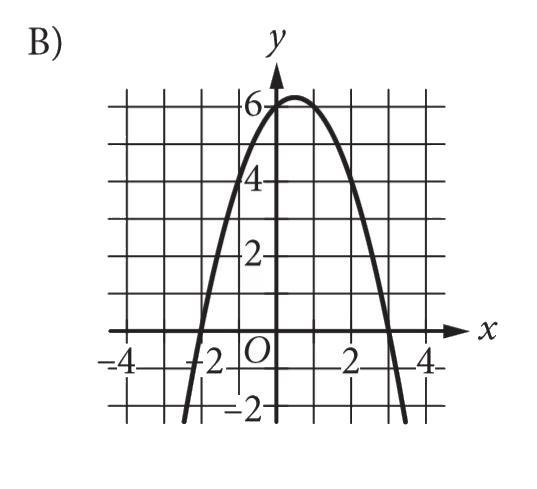
B
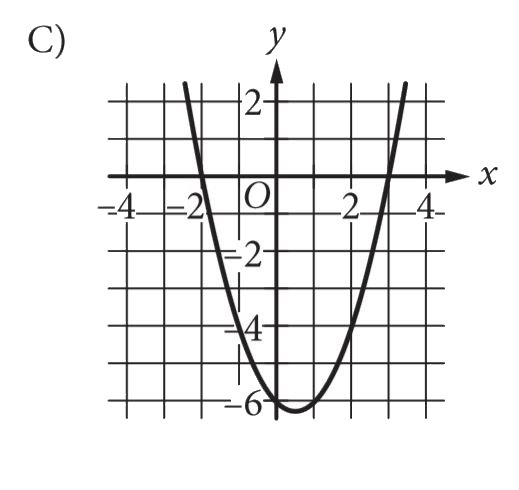
C
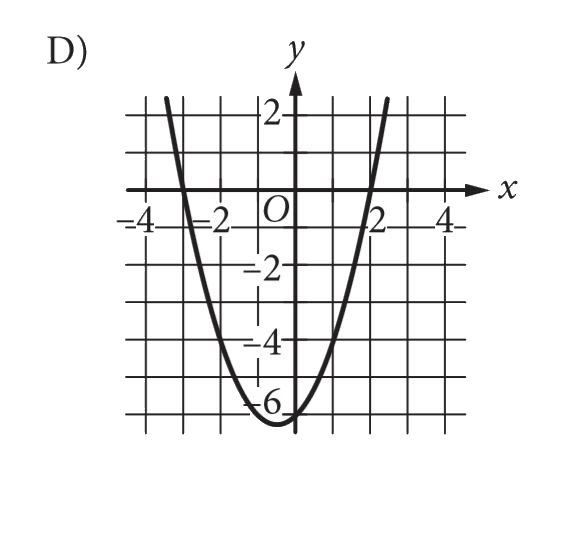
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- f (x) = (x + 3)(x − k) T he function f is defined above. If k is a p...
Text Solution
|
- The graph of the function y=f(x). Then which of the following could re...
Text Solution
|
- If a function y=f(x) such that f'(x) is continuous function and satisf...
Text Solution
|
- Given a function, f(x), such that f(x) = f(|x|). Which one of the fo...
Text Solution
|
- If the accomanying figure above shows the graph of function f, which o...
Text Solution
|
- The graph of y=f(x) is shown below. Which of the following could ...
Text Solution
|
- The graph of the function f is shown above. Which of the following cou...
Text Solution
|
- Question 1 and 2 refer to the information and graph below. Let funct...
Text Solution
|
- The function f is defined by f (x) = (x + 3)(x + 1). The graph of f in...
Text Solution
|