Similar Questions
Explore conceptually related problems
Recommended Questions
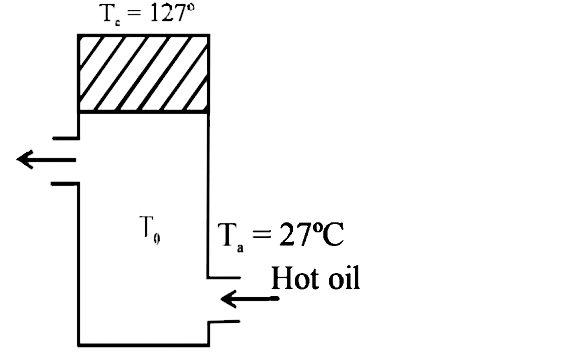
- Hot oil is circulated thorugh an insulated container with a wooden lid...
Text Solution
|
- Calculate the amount of heat radiated per second by a body of surface ...
Text Solution
|
- Hot oil is circulated thorugh an insulated container with a wooden lid...
Text Solution
|
- The top of an insulated cylindrical container is covered by a disc hav...
Text Solution
|
- A black body at temperature 227^(@)C radiates heat at the rate of 5 ca...
Text Solution
|
- एक कृष्ण वस्तु का ताप 127^@C है। यह वस्तु एक अन्य कृष्ण वस्तु से घिरी...
Text Solution
|
- एक ऊष्मारोधी बेलनाकार बर्तन ऊपर से 1 सेमी मोटाई की चकती से ढाका है चकत...
Text Solution
|
- Water of volume 2 L in a container is heated with a coil of 1 kW at 27...
Text Solution
|
- An insulated container has a wooden lid at the top whose conductivity ...
Text Solution
|