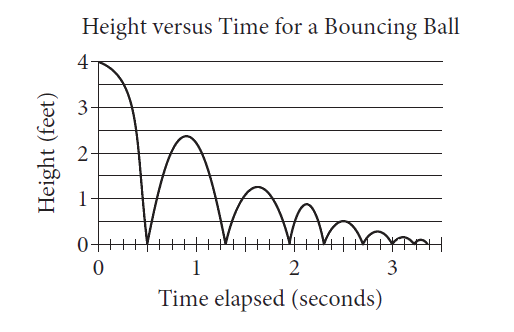
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- As part of an experiment, a ball was dropped and allowed to bounce rep...
Text Solution
|
- A ball is dropped from height 5m. The time after which ball stops rebo...
Text Solution
|
- The inequation represented by the graph given below is : <img src="htt...
Text Solution
|
- As part of an experiment, a ball was dropped and allowed to bounce rep...
Text Solution
|
- A ball is dropped from height h on the ground where co-efficient of re...
Text Solution
|
- Two balls are dropped to the ground from different heights.The second ...
Text Solution
|
- Two balls are dropped to the ground from different heights. One ball i...
Text Solution
|
- Two balls are dropped to the ground from different heights .One ball i...
Text Solution
|
- Two balls are dropped to the ground from different heights.One ball is...
Text Solution
|