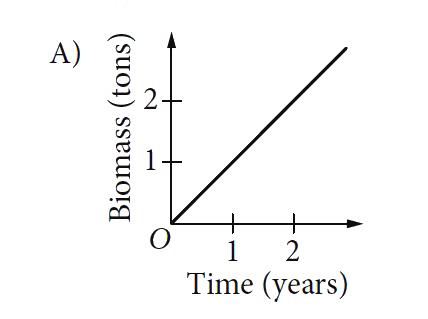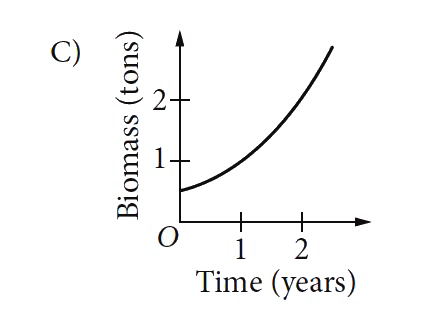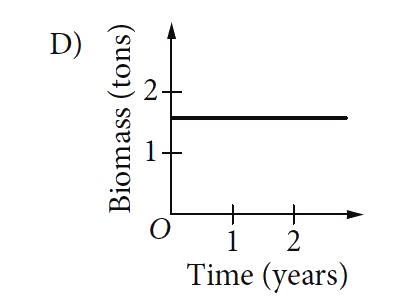A
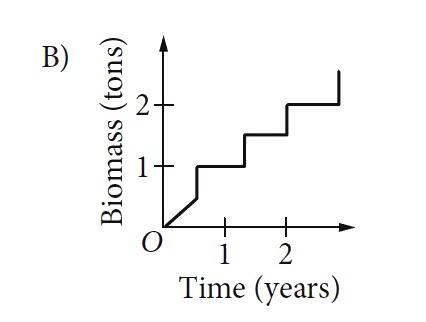
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Recommended Questions
- The mass of living organisms in a lake is defined to be the biomass of...
Text Solution
|
- A square lake has a tree at each corner.How can you double the area of...
Text Solution
|
- A square lake has a tree at each corner.How can you double the area of...
Text Solution
|
- A square lake has a tree at each corner.How can you double the area of...
Text Solution
|
- A square lake has a tree at each corner.How can you double the area of...
Text Solution
|
- The organisms which live in the bottom of lake are called:
Text Solution
|
- In a lake ecosystem, pyramid of biomass is:
Text Solution
|
- What does the imaginary line passing through Lake Ontario, Lake Erie, ...
Text Solution
|
- Organisms living at the bottom of a lake are
Text Solution
|