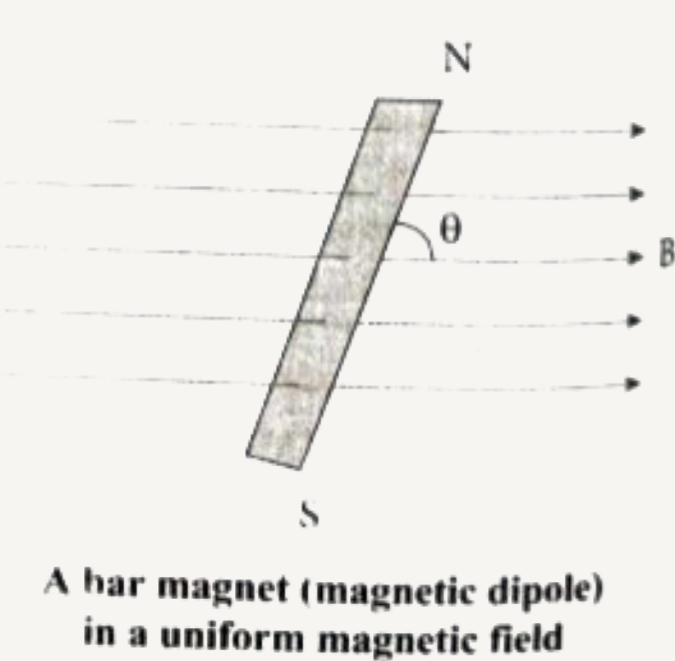
When a bar magnet ( magnetic dipole) of dipole moment `vecp_(m) ` is held at an angle `theta` with the direction of a uniform magnetic field `vecB`, as shown in Figure the magnitude of the torque acting on the dipole is

`|vectau_(B)| = |vecp_(m)||vecB|sin theta `
If the dipole is rotated through a very small angular displacement `d theta ` against the torque `tau_(B) ` at constant angular velocity, then the work done by external torque `(vectau_("ext"))` for this small angular displacement is given by
`dW = |vectau_("axt")|d theta `
Since the bar magnet to be moved at constant angular velocity , it implies `|vectau_(B)|=|vectau_("ext")|`
` dW = p_(m) B sin theta d theta`
Total work done in rotaiting the dipole from `theta'" to " theta ` is
`W = underset(theta)overset(theta)int tau d theta = underset(theta)overset(theta)intp_(m) B sin theta d theta = p_(m) B [ - cos theta d theta ]_(theta )^(theta ) `,
`W = p_(m) B ( cos theta - cos theta')`
This work done is stored as potential energy in bar magnet at an angle `theta` when it is rotated from `theta'" to " theta` and it can be written as
`U = p_(m) B ( cos theta - cos theta')` ....(1)
In fact, the equation (1) gives the difference in potential energy between the angular position `theta'` and `theta ` . We can choose the reference point `theta' = 90^(@) ` , so that second term in the equation becomes zero and the equation (1) can be written as
` U = - p_(m) B ( cos theta ) ` ....(2)
The potential energy stored in a bar magnet in a uniform magnetic field is given by
` U = - vecp_(m) * vecB ` .......(3)
Case 1
(i) If `theta = 0^(@) , ` then
` U = p_(m) B ( cos 0^(@)) = - p_(m) B `
(ii) If ` theta = 180^(@) `, then
` U = p_(m) B ( cos 180^(@)) = p_(m) B `
We can infer from the above two results , the potential energy of the bar magnet is minimum when it is aligned along the external magnetic field and maximum when the bar magnet is aligned anti - parallel to external magnetic field.