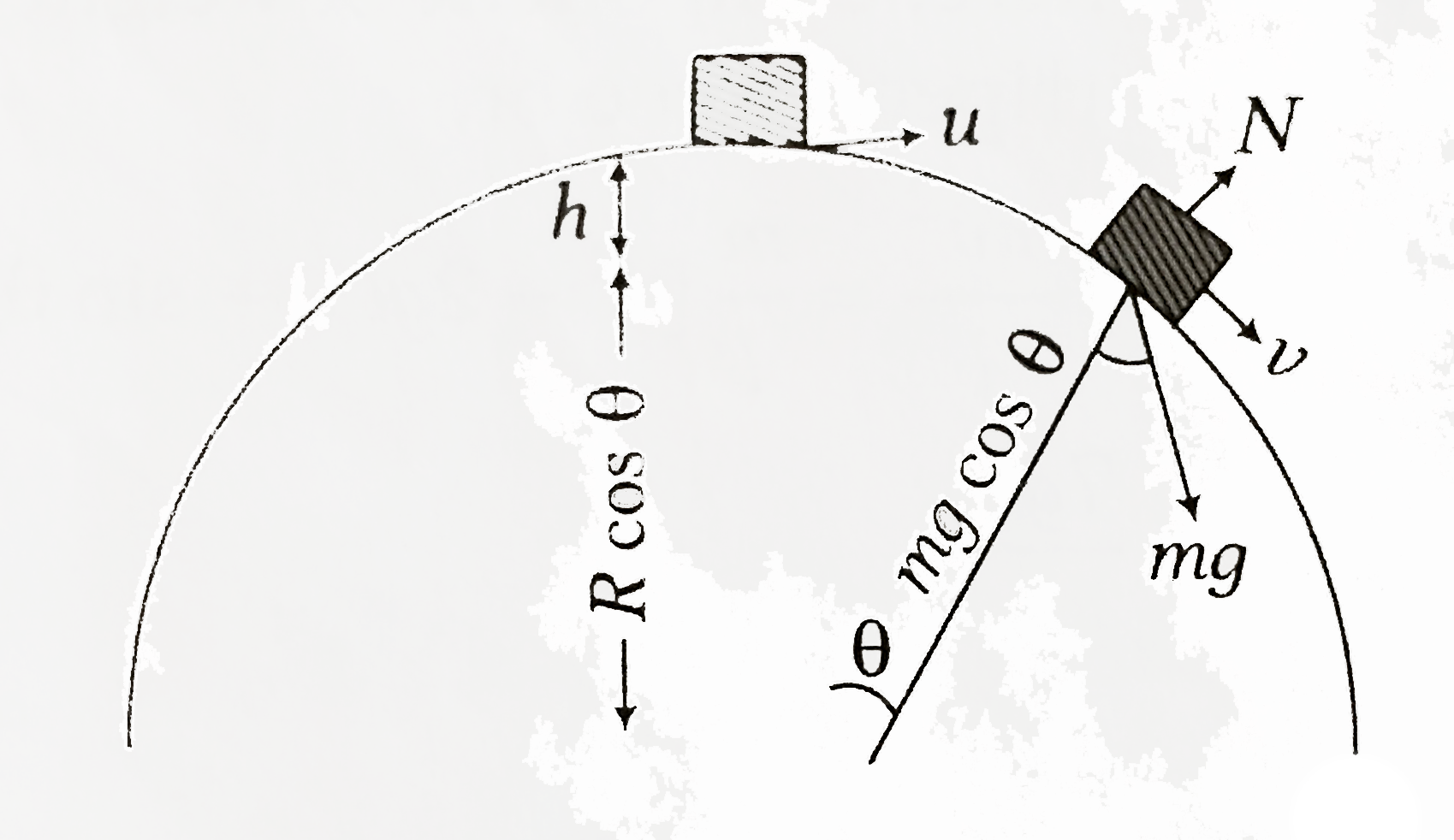
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A particle of mass m is released from the top of a smooth hemisphere o...
Text Solution
|
- A particle rests on the top of a smooth hemisphere of radius r . It is...
Text Solution
|
- A hemisphere of radius R and of mass 4m is free to Slide with its base...
Text Solution
|
- A particle is released from the top of a smooth hemisphere.find the an...
Text Solution
|
- A particle of mass m is released from the top of a smooth hemisphere o...
Text Solution
|
- A particle of mass m is released on a fixed. Smooth sphere of radius R...
Text Solution
|
- A particle is released from the top of the smooth hemisphere R as show...
Text Solution
|
- A small body of mass m slides without friction from the top of a hemi...
Text Solution
|
- A hemisphere of radius R and mass 4 m is free to slide with its base o...
Text Solution
|