Home
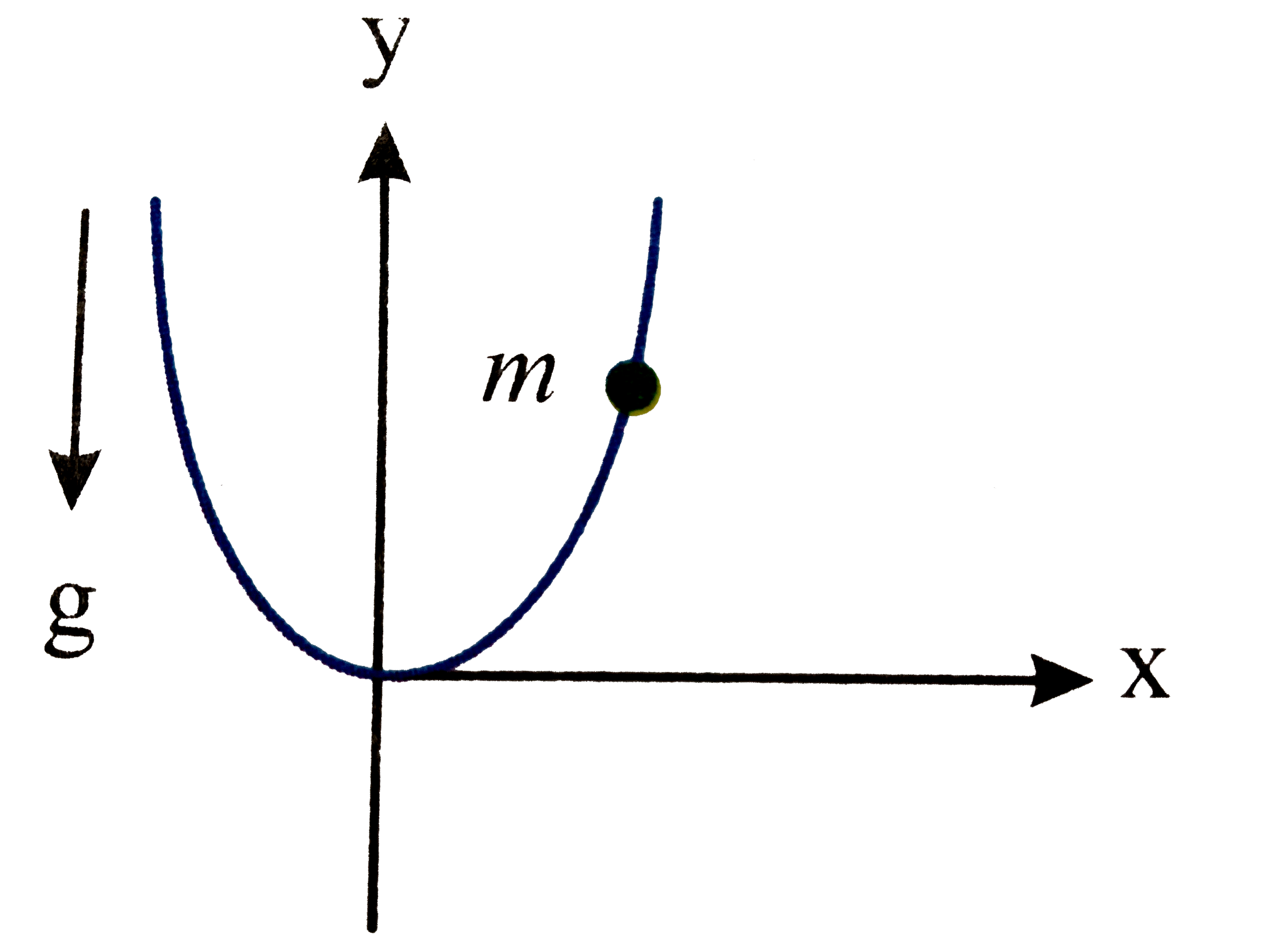
Class 11
PHYSICS
A particle of mass m is allowed to oscil...

A particle of mass `m` is allowed to oscillate near the minimum of a vertical parabolic path having the equaiton `x^(2) =4ay`. The angular frequency of small oscillation is given by

A

`sqrt(gh)`

B

`sqrt(2gh)`

C

`sqrt(((g)/(2a)))`

D

`sqrt(((g)/(a)))`

Text Solution

Verified by Experts

The correct Answer is:
C
At the vertex, tangential acceleration is zero. When particle is at mean position, it is at vertex. When it is displaced for small angle `theta`,
`-mf=mg sin theta`
or `f=-g sin theta=-g theta tan theta`
or `f=-g((dt)/(dx))`
`because" "x^(2)=4ay or 2x =42(dy)/(dx)`
`or" " (dy)/(dx)=(x)/(2a)therefore tantheta=(x)/(2a)`

`therefore" "f=-g((x)/(2a))`
or `-omega^(2)x=-g((x)/(2a))`
`therefore" "omega=sqrt(((g)/(2a)))`
Promotional Banner

Topper's Solved these Questions

  • SIMPLE HARMONIC MOTION

    BITSAT GUIDE|Exercise BITSAT Archives|12 Videos

  • SCALARS AND VECTORS

    BITSAT GUIDE|Exercise All Questions|34 Videos

  • TRANSMISSION

    BITSAT GUIDE|Exercise All Questions|38 Videos

Similar Questions

Explore conceptually related problems

A point mass m is displaced slightly from point O and released. It is constrained to move along parabolic path having equation x^(2)=ky then its angular frequency of oscillation is :

A simple harmonic motion is represented by x(t) = sin^2 omegat - 2 cos^(2) omegat . The angular frequency of oscillation is given by

A simple harmonic motion is represented by x(t) = sin^(2)omega t - 2 cos^(2) omega t . The angular frequency of oscillation is given by

A particle of mass m moves in a one dimensional potential energy U(x)=-ax^2+bx^4 , where a and b are positive constant. The angular frequency of small oscillation about the minima of the potential energy is equal to

The equation of a damped simple harmonic motion is m(d^2x)/(dt^2)+b(dx)/(dt)+kx=0 . Then the angular frequency of oscillation is

If a simple harmonic oscillator has got a displacement of 0.02 m and acceleration equal to 0.02m//s^(2) at any time, the angular frequency of the oscillator is equal to:

For a simple harmonic oscillator, the aceeleration is 3 m//s^(2) when the displacement is 0.03 m. The angular frequency of the oscillator is

From the given figure find the frequency of oscillation of the mass m

If at some instant of time, the displacement of a simple harmonic oscillator is 0.02 m and its acceleration is 2ms^(-2) , then the angular frequency of the oscillator is

A block of mass m connected with a smooth perismatic wedge of mass m is released from rest when the spring is relaxed. Find the angular frequency of oscillation.