Home
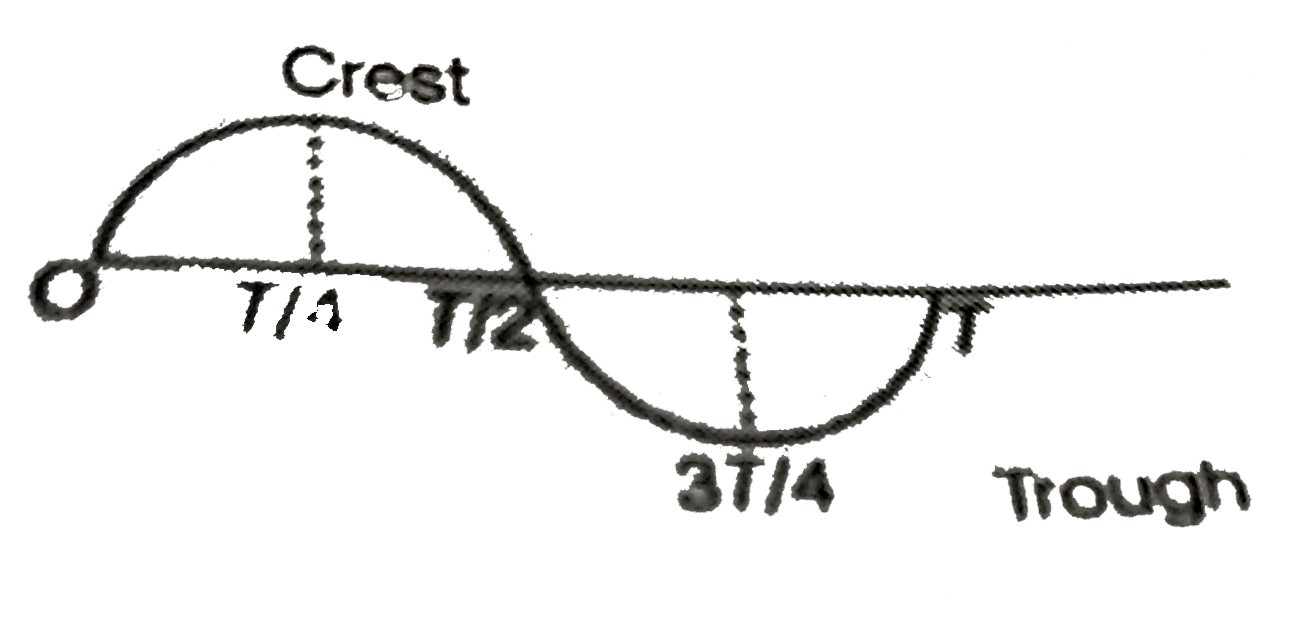
Class 11
PHYSICS
A particle on the trough of a wave at an...

A particle on the trough of a wave at any instant will come to the mean position after a time ( T = time period)

A

`T//2`

B

`T//4`

C

T

D

2 T

Text Solution

Verified by Experts

The correct Answer is:
B
The time taken by the particle to come to mean position from the trough = `(T)/(4)`
Promotional Banner

Topper's Solved these Questions

  • WAVE MOTION

    BITSAT GUIDE|Exercise BITSAT Archives|8 Videos

  • UNITS, MEASUREMENTS & DIMENSION

    BITSAT GUIDE|Exercise All Questions|58 Videos

Similar Questions

Explore conceptually related problems

A particle starts simple harmonic motion from the mean position. If It's amplitude is A and time period T, then at a certain instant, its speed is half of its maximum speed at this instant, the displacement is

Two pendulum of lengths 1m and 16m are in phase at the mean position at a certain instant of time. If T is the time period of the shorter pendulum, then the minimum time after which they will again be in phase is

The distance between consecutive crest and trough of a wave is 10 cm . If the speed of wave is 200 cm/s . Then the time period of wave is

A particle startsits SHM at t=0 . At a particular instant on its way to extreme position , x= (A)/(2) . Find the time taken by the particle to come back to this point after passing through the extreme position. Hint : t_(1) = time taken to go from x=0 to x= (A)/(2) t_(2) = time taken to go to extreme position and come back to mean position = (T)/(2) Required time = (T)/(2) - t_(1)

A particle is in SHM with time period 3 sec. Calculate the displacement of particle from mean position after t = 0.5 sec.

The time period of a particle executing S.H.M. is 1 s. If the particle starts motion from the mean position, then the time during which it will be at mid way between mean and extreme position will be

A particle executing simple harmonic motion has a time period of 4 s. If the particle starts moving from the mean position at t = 0, then after how much interval of time from t = 0, will its displacement be half of its amplitude ?

A particle executes a linear S.H.M. of amplitude A and period T. It starts from the mean position. The time required to cover a dis"tan"ce A/2 is