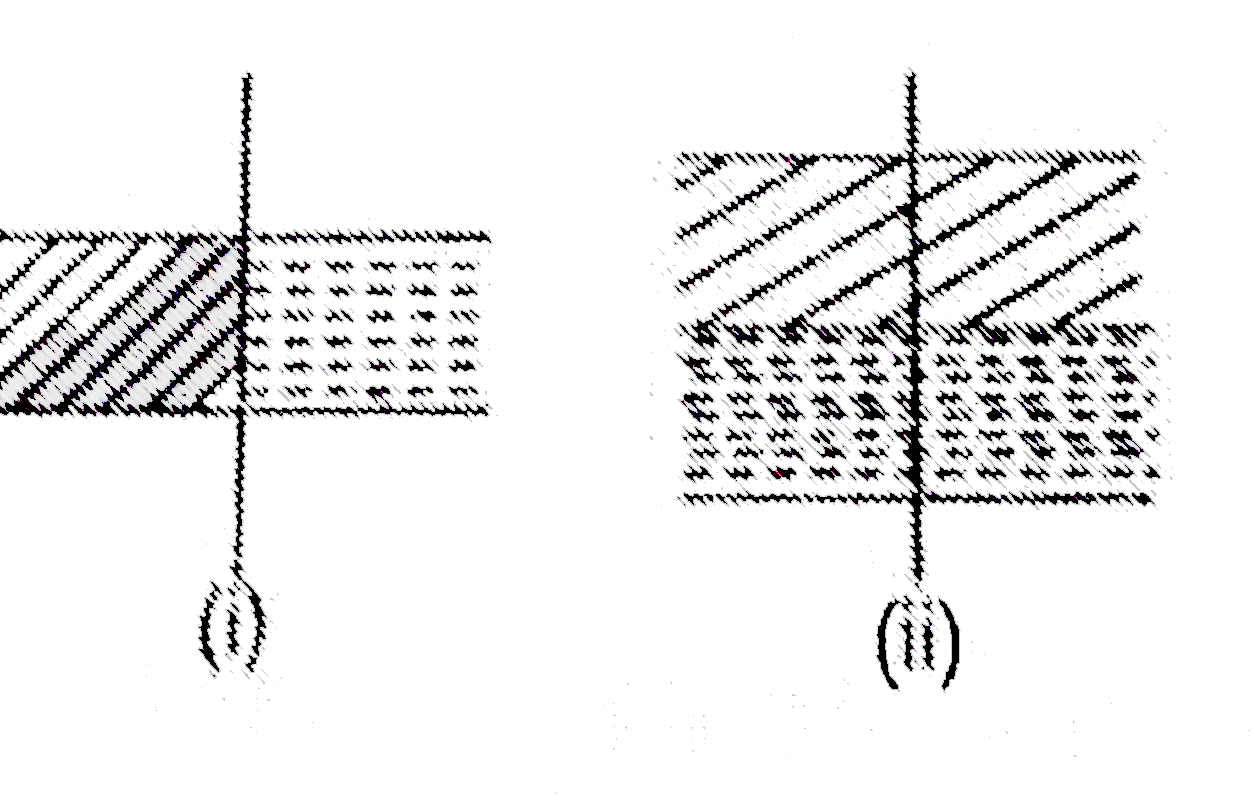A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
BITSAT GUIDE-ELECTRIC CAPACITOR-BITSAT archives
- Calculate the ratio of capacitance of two capacitors of same dimension...
Text Solution
|
- Three capacitors X = 1 muF, Y = 2 muF and Z = 3 muF are connected as s...
Text Solution
|
- A capacitor of capacity 0.1 muF connected in series to a resistor of 1...
Text Solution
|
- The work done in placing a charge of 8xx10^-18 coulomb on a condenser ...
Text Solution
|
- Two identical air filled parallel plate capacitors are charged to the ...
Text Solution
|
- Which of the following is discontinuous across a charged conducting su...
Text Solution
|
- Capacitance of a capacitor made by a thin metal foil is 2 muF. If the ...
Text Solution
|