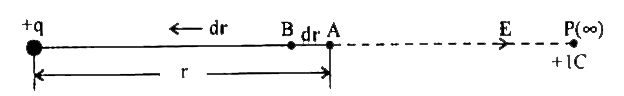Text Solution
Verified by Experts
Topper's Solved these Questions
ELECTROSTATIC POTENTIAL AND CAPACITANCE
SUBHASH PUBLICATION|Exercise FIVE MARKS QUESTIONS WITH ANSWER|3 VideosELECTROSTATIC POTENTIAL AND CAPACITANCE
SUBHASH PUBLICATION|Exercise NUMERICALS WITH SOLUTIONS|20 VideosELECTROSTATIC POTENTIAL AND CAPACITANCE
SUBHASH PUBLICATION|Exercise TWO MARKS QUESTIONS WITH ANSWERS|1 VideosELECTROMAGNETIC WAVES
SUBHASH PUBLICATION|Exercise ONE MARK QUESTIONS WITH ANSWERS|36 VideosII PUC ANNUAL EXAMINATION QUESTION PAPER MARCH 2019
SUBHASH PUBLICATION|Exercise QUESTION|34 Videos
Similar Questions
Explore conceptually related problems
SUBHASH PUBLICATION-ELECTROSTATIC POTENTIAL AND CAPACITANCE -THREE MARKS QUESTION WITH ANSWER
- Draw a neat labelled diagram of van de graaff generator. Give the prin...
Text Solution
|
- Give any three applications of Van der Graaff generator.
Text Solution
|
- Derive a relation between electric field and potential
Text Solution
|
- Give the expression for the potential energy of a dipole in an externa...
Text Solution
|